初等数学公式集/初等幾何/表面積

このページでは立体図形の表面積等の公式についての解説をします。

直方体の表面積

$S=2(ab+bh+ha)$

直方体の底面積

$B=ab$

直方体の側面積

$A=a{h}(a+b)$

立方体の表面積

$S=6{a}^{2}$

柱体の側面積

$S=lh$

直角三角錐(3直角四面体)

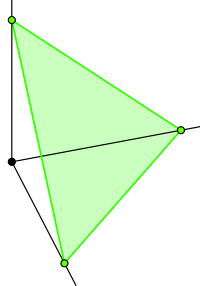直角三角錐(3直角四面体)

三角錐$OABC$において，1つの頂点$O$に集まる3つの角 $\angle AOB$ ， $\angle BOC$ ， $\angle COA$ がいずれも直角である三角錐を直角三角錐(3直角四面体)と定義し、$OA=a,OB=b,OC=c$（ただし$abc\neq {0}$とする）であるものとする。

$\angle AOB$ ， $\angle BOC$ ， $\angle COA$ より、この立体の各頂点は、$O$$(0,0,0)$,　$A$$(a,0,0)$,　$B$$(0,b,0)$,　$C$$(0,0,c)$とおける。

3点 $x$切片$(a,0,0)$, $y$切片$(0,b,0)$, $z$切片$(0,0,c)$を通る平面$P$の式は、

$P:{\frac {x}{a}}+{\frac {y}{b}}+{\frac {z}{c}}=1$である。 - 初等数学公式集/解析幾何#平面の式参照

原点$O$$(0,0,0)$と平面$P:{\frac {x}{a}}+{\frac {y}{b}}+{\frac {z}{c}}-1=0$の距離$h$:

$h={\frac {|-1|}{\sqrt {{\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}+{\frac {1}{c^{2}}}}}}={\frac {1}{\sqrt {\frac {a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}}{a^{2}b^{2}c^{2}}}}}={\frac {abc}{\sqrt {a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}}}}$

三角錐$OABC$の体積を$V$とすると、$V={\frac {abc}{6}}$

ここで、$\triangle ABC$の面積$S$とすると、$V={\frac {hS}{3}}$であり、従って、$S={\frac {abc}{2h}}$

$S={\frac {abc}{2}}{\dot {\frac {\sqrt {a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}}}{abc}}}={\frac {\sqrt {a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}}}{2}}$

• 両辺2乗すると、

  $S^{2}=\left({\frac {ab}{2}}\right)^{2}+\left({\frac {bc}{2}}\right)^{2}+\left({\frac {ca}{2}}\right)^{2}$

  　

  即ち、$S_{\triangle ABC}^{2}=S_{\triangle OAB}^{2}+S_{\triangle OBC}^{2}+S_{\triangle OCA}^{2}$が成立している。これは、三平方の定理を3次元空間に拡張したものと言えド・グアの定理通称「四平方の定理」と言われる。

球の表面積・冠形/球台の曲線部の表面積

球の表面積

1. 球の体積より

   $V={\frac {4}{3}}\pi r^{3}$

   これを、$r$について微分すると、${\frac {dV}{dr}}=4\pi r^{2}$

   　

2. 積分による方法

   $x^{2}+y^{2}+z^{2}=r^{2}$である球から、$z=0$で切断した面を想定する。

   原点から成す角を$\theta$として円周上の点$A(r\cos \theta ,r\sin \theta )$とし、$\theta$をわずかに$d\theta$変化させた$A'(r\cos(\theta +d\theta ),r\sin(\theta +d\theta ))$を考える。この時、$AA'$の距離は、$d\theta$がわずかな値であるため、$rd\theta$に近似される。

   ここで、$AA'$を$x$軸を中心に回転させると、$A,A'$各々が、周の長さ$2\pi r\sin \theta ,2\pi r\sin(\theta +d\theta )$である帯状の図形を得、

   その面積は、$s={\frac {1}{2}}(2\pi r\sin \theta +2\pi r\sin(\theta +d\theta ))\cdot rd\theta$

   $d\theta$は微小で限りなく$0$に近づくため、加算において$\sin \theta =\sin(\theta +d\theta )$としてよく、その結果、$s=2\pi r^{2}\sin \theta d\theta$とおける。

   ここで、$\theta$について、区間$\left[0,{\frac {\pi }{2}}\right]$で積分することにより、球の$x\geq 0$の部分の表面積が得られる。

   $S_{hemi}=\int _{0}^{\frac {\pi }{2}}2\pi r^{2}\sin \theta d\theta$$=2\pi r^{2}\int _{0}^{\frac {\pi }{2}}\sin \theta d\theta$$=-2\pi r^{2}\left[\cos \theta \right]_{0}^{\frac {\pi }{2}}$$=2\pi r^{2}$

   　　

   この球は$x=0$について対称であり、$x<0$の部分の表面積も等しいので、$S=2S_{hemi}=4\pi r^{2}$

   　

   • 積分を使った誤答の例

     $x^{2}+y^{2}+z^{2}=r^{2}$である球を考える。

     $x=t$でこの球を切断すると、半径${\sqrt {r^{2}-t^{2}}}$である円;$C$を得、この円;$C$の円周は$2\pi {\sqrt {r^{2}-t^{2}}}$である。

     球の表面積は、この周に微細な幅$dt$をかけた$2\pi {\sqrt {r^{2}-t^{2}}}dt$^※を区間$[-r,r]$で累積したものであるから、その区間で積分することにより得られる。

     $S=\int _{-r}^{r}2\pi {\sqrt {r^{2}-t^{2}}}\,dt$$=4\pi \int _{0}^{r}{\sqrt {r^{2}-t^{2}}}\,dt$

     $t=r\sin \theta$とおく、微分して$dt=r\cos \theta d\theta$

     （与式）$=4\pi \int _{0}^{\frac {\pi }{2}}{\sqrt {r^{2}-r^{2}\sin ^{2}\theta }}\cdot r\cos \theta d\theta$$=4\pi r^{2}\int _{0}^{\frac {\pi }{2}}{\sqrt {1-\sin ^{2}\theta }}\cdot \cos \theta d\theta$ $=4\pi r^{2}\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos ^{2}\theta }}\cdot \cos \theta d\theta$

     $=4\pi r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta d\theta$$=4\pi r^{2}\left[{\frac {2\theta +\sin 2\theta }{4}}\right]_{0}^{\frac {\pi }{2}}$$=\pi ^{2}r^{2}$

     となって、誤答を得る。これは、「周に微細な幅$dt$をかけたもの（※）」の面積は、正しくは、${\frac {1}{2}}\left(2\pi {\sqrt {r^{2}-t^{2}}}+2\pi {\sqrt {r^{2}-(t+dt)^{2}}}\right)dt$であって、括弧内後項の$dt$は積分において無視できなくなることの立式の誤りである。

     　　　

冠形の曲線部の表面積

球冠

• 球冠（平面により切断された球の一部）の曲面部の表面積$S$:

  関係する諸数値を以下のものとする（右図参照）。

  • 球の半径 $r$
  • 球冠の底の半径 $a$
  • 球冠の高さ $h$
  • 球の中心から球冠の頂点（極）までの線と球冠の底を形作る円板の端との間の極角 $\theta$

1. 極角 $\theta$が与えられている場合

   上記の球の表面積を積分を用い求める解法を用い、区間$\left[0,\theta \right]$で積分することで求められる。

   $S=2\pi r^{2}\int _{0}^{\theta }\sin xdx$$=-2\pi r^{2}\left[\cos x\right]_{0}^{\theta }$$=2\pi r^{2}(1-\cos \theta )$（※2）

2. $r$ と $h$ が与えられている場合

   $\cos \theta ={\frac {r-h}{r}}$であるから、※2に代入して、$S=2\pi r^{2}(1-\cos \theta )$$=2\pi r^{2}\left(1-{\frac {r-h}{r}}\right)$$=2\pi r^{2}\left({\frac {r-r+h}{r}}\right)=2\pi rh$（※3）

3. $a$ と $h$ が与えられている場合

   $r^{2}=a^{2}+(r-h)^{2}$から、$r={\frac {a^{2}+h^{2}}{2h}}$

   ※3に代入して、$S=2\pi rh$$S=2\pi h\left({\frac {a^{2}+h^{2}}{2h}}\right)$$=\pi (a^{2}+h^{2})$（※4）

球台の曲線部の表面積

球台

• 球台（球を1対の平行な平面で切断した立体/先端が切り取られた球冠）の曲面部（球帯）の表面積$S$:

  関係する諸数値等を以下のものとする（右図参照）。

  • もとの球の半径 $R$、球の中心を$O$
  • 球台の底の各々の半径 $r_{1},r_{2}$、底の中心を各々$A,B$、直線$AB$と球との交点を$C,D$とする、なお$DABC$の順に並ぶ。
  • 球台の高さ（2つの平行な底面間の距離） $H$

1. $R$ と $r_{1},r_{2}$ が与えられている場合
   1. 球を切断する平行な2平面の外に球の中心がある場合（ただし、$r_{1}>r_{2}$）

      中心$A$の円が底である冠形について、高さ$AC$は、$R-{\sqrt {R^{2}-r_{1}^{2}}}$

      ※4より、この冠形の曲面部表面積$S_{A}$は、$\pi (r_{1}^{2}+AC^{2})$$=\pi \left(r_{1}^{2}+\left({R-{\sqrt {R^{2}-r_{1}^{2}}}}\right)^{2}\right)$$=\pi \left(r_{1}^{2}+R^{2}-2R{\sqrt {R^{2}-r_{1}^{2}}}+R^{2}-r_{1}^{2}\right)$$=\pi \left(2R^{2}-2R{\sqrt {R^{2}-r_{1}^{2}}}\right)$

      同様に、中心$B$の円が底である冠形の曲面部表面積$S_{B}$は、$=\pi \left(2R^{2}-2R{\sqrt {R^{2}-r_{2}^{2}}}\right)$

      求める球台の曲面部表面積は、これらの球冠の曲面部表面積の差であるから、

      $S_{A}-S_{B}$$=\pi \left(2R^{2}-2R{\sqrt {R^{2}-r_{1}^{2}}}\right)-\pi \left(2R^{2}-2R{\sqrt {R^{2}-r_{2}^{2}}}\right)$$=2\pi R\left({\sqrt {R^{2}-{r_{2}}^{2}}}-{\sqrt {R^{2}-{r_{1}}^{2}}}\right)$（※5）

   2. 球を切断する平行な2平面の外に球の中心がある場合

      $O$を通る$CD$と直行する平面で球を分割。

      中心$A$の円と分割によりできた円を各々底とする球台の曲面部表面積は、半球の曲面部表面積から中心$A$の円が底である冠形の局面部表面積を引いたものであるので、

      $S_{A}=2\pi R^{2}-\pi \left(2R^{2}-2R{\sqrt {R^{2}-r_{2}^{1}}}\right)$$=2\pi R\left({\sqrt {R^{2}-r_{1}^{2}}}\right)$

      同様に$S_{B}=2\pi R\left({\sqrt {R^{2}-r_{2}^{2}}}\right)$

      したがって、$S=S_{A}+S_{B}=2\pi R\left({\sqrt {R^{2}-{r_{1}}^{2}}}+{\sqrt {R^{2}-{r_{2}}^{2}}}\right)$（※6）

2. $R$ と $h$ が与えられている場合

   以下により、$S=2\pi Rh$

   1. 点の順が$OABC$である時、

      $h=OB-OA$であるので、上の例同様、球台の底のうち、$A$を中心とする円の半径を$r_{1}$、$B$を中心とする円の半径を$r_{2}$とすると、

      $h=OB-OA={\sqrt {R^{2}-{r_{2}}^{2}}}-{\sqrt {R^{2}-{r_{1}}^{2}}}$

      ※5に代入して、$S=2\pi Rh$

   2. 点の順が$AOBC$である時、

      $h=OA+OB$であるので、上の例同様、球台の底のうち、$A$を中心とする円の半径を$r_{1}$、$B$を中心とする円の半径を$r_{2}$とすると、

      $h=OA+OB={\sqrt {R^{2}-{r_{1}}^{2}}}+{\sqrt {R^{2}-{r_{2}}^{2}}}$

      ※6に代入して、$S=2\pi Rh$

円環体（トーラス）の表面積

円環体・トーラス

半径$r$の円;$C$を、円の中心からの距離$R$（但し、$r$　≦　$R$とする）の直線を軸として回転させた円環体（トーラス、ドーナツ型）の表面積

$S=4\pi ^{2}rR=(2\pi r)(2\pi R)$

体積の公式;$V=2\pi ^{2}r^{2}R$に関して、半径$r$について微分することにより得られる。