高等学校物理/物理II/電気と磁気

静電誘導と誘電分極

コンデンサー

詳細は「高等学校物理/物理I/電気#コンデンサー」を参照

誘電体

まず、高校物理でいう「誘電体」（ゆうでんたい）とは、通常のセラミック、雲母（マイカ）など電気を通さない物質のうち高い誘電率を示すものです。

金属は導体なので誘電体ではありません。

では、誘電体の物理について、説明します。

誘電体を入れたコンデンサー

コンデンサーに誘電体を入れると、誘電体が誘電分極を起こすため、コンデンサのプラス極板で発生した電気力線のいくつかが打ち消されます。

その結果、誘電体の入ったコンデンサーの極板間の電場は、極板の電荷密度で発生する電荷が真空中でつくる電場よりも弱くなります。

この結果、静電容量が変わます。

さて、真空中の静電容量の公式は、

$C=\varepsilon _{0}{\frac {S}{d}}$

でした。

誘電体のある場合の静電容量は、

$C=\varepsilon {\frac {S}{d}}$

となります。

ここで、 $\varepsilon$を誘電率（ゆうでんりつ）といいます。 $\varepsilon _{0}$を、真空中の誘電率といいます。

物質の比誘電率

物質	比誘電率
空気 (20℃)	1.0005
パラフィン (20℃)	2.2
ボール紙 (20℃)	3.2
雲母	7.0
水 (20℃)	約80
チタン酸バリウム	約5000

ここで、比

$\varepsilon _{r}={\frac {\varepsilon }{\varepsilon _{0}}}$

を、比誘電率（ひ ゆうでんりつ）といいます。

つまり、$\varepsilon _{r}$ は比誘電率です。 いっぽう、 $\varepsilon _{0}$ および $\varepsilon$ は、比誘電率ではありません。

比誘電率 $\varepsilon _{r}$ をもちいれば、静電容量 C の式は、

$C=\varepsilon {\frac {S}{d}}=\varepsilon _{r}\varepsilon _{0}{\frac {S}{d}}$

と書けます。

コンデンサの静電エネルギー

U=2⁻¹CV²

=2⁻¹QV
=(2C)⁻¹Q²

電流による磁界

磁石のまわりには物体を動かす力のあるものが生じています。 これを磁場（じば）と呼ぶ。磁界（じかい）ともいう。

電流が流れているときにも、そのまわりには、右ねじの法則（right-handed screw rule）に従う向きに磁界が生じます。 電流I[A]が直線的に流れているとき、磁界の大きさは $B={\frac {\mu _{0}}{2\pi a}}I$ であることが知られています。

ここで、aは磁束密度を測る点と、電線の距離。

また、$\mu _{0}$は真空の透磁率（とうじりつ、permeability）を表し、値は $4\pi \times 10^{-7}$[H/m] です。

電磁誘導と電磁波

電磁誘導

磁場を伴う物体が運動すると、そのまわりには電場が生じることを電磁誘導（でんじゆうどう、electromagnetic induction）といいます。 仮に、ソレノイド（solenoid、コイルのこと）の近くでそれを行なったとすると、生じた電場によってソレノイドの中には電流が流れます。 生じる電場の大きさは、 ${\vec {E}}={\frac {1}{2\pi a}}{\frac {d{\vec {B}}}{dt}}$ となります。(半径aの円形のコイルの場合。) Eの単位は[V/m]であり、Bの単位は[T]です。

電磁波

磁場の動きによって電場が引き起こされることを電磁誘導のセクションで見た。

また、実際には電場の変化によって磁場が引き起こされることも実験によって知られています。 これによって何もない空間中を電場と磁場が伝播していくことが予想されます。

(:電磁波の伝播のschematicな絵)

※ 市販の大学生むけ教科書を読んでも、ロクにヘルツの実験を説明してないので、高校側で説明します。

※ なお、高校では専門『物理』で習う内容。

まず、物理実験家ヘルツは放電実験により、受信機を回路中にギャップのある回路として、送信側の放電による電場が遠隔的に離れた位置にある受信側の回路に伝わることを確認した。

この実験の際、ヘルツは受信回路の向きをいろいろと変えて実験したことにより、送信機の向きに対しての受信機の向きによって電場の伝わり方が異なることから、電場の遠隔作用に偏光性がある事が分かった。

（※ 範囲外）なお、方解石などに偏光作用のあることは、すでにこの時代に分かっていたと思われます。

電場のこの作用には偏光性があるので、波であるとみなすことは妥当でしょう。

ヘルツの実験から、実験的にわかることとして

電場は遠隔作用で伝わること

放電は電場の遠隔作用を生じさせること

その電場の遠隔作用には、偏光作用のあること

が実験的にわかります。

物理学では、ヘルツの実験の以前から、理論物理学者のマクスウェルにより、

電磁波という、電場と磁場の相互作用によって真空中を伝達する予測されていた。

なので、ヘルツの実験は、マクスウェルの予測した電磁波だとみなされた。 現代でも物理学者は、そうみなしています。

なお、マクスウェルが理論計算で求めた電磁波の速度を求めたところ、すでに知られていた光速の大きさ（およそ 3×10⁸ m/s ）に精度よく一致した。

このことからも、光は電磁波の一種であることが分かります。

（啓林館の教科書にある余談: ）余談ですが、人類初の無線通信に成功した人物はマルコーニです（ヘルツではないので、誤解しないように）。

ヘルツの実験では、厳密には少なくとも放電の電場が伝わることしか観測できてませんが、しかし磁場もこの実験で伝わると考えても支障が生じて無いし、実際に人類には支障は生じてないので、今でもヘルツの実験がマクスウェルの予測した電磁波の証明の実験として伝えられています。

なお、光には、反射や屈折や回折や、ヤングスリットの回折などがあるが、

ヘルツの放電実験のような電磁波の火花放電の実験でも、光の実験と同様の配置で、金属板を配置して確認することで、電磁波も反射や屈折や回折や、ヤングスリットの回折などの現象も起こすことが、実験的にも確認されています（※ 参考文献 :実教出版の専門『物理』の検定教科書）（※ ヤングのスリットの電磁波実験に関しては啓林館の教科書『物理』にあります）。

これらのことからも、光は電磁波の一種であるとみなすのが妥当であることが分かります。

（※ 範囲外 :）また、電磁波の反射を利用して、電磁波の波長を測定することにヘルツは成功した。電磁波を反射させれば、やってくる波と干渉して定常波ができるはずです。ヘルツの実験例では受信機を送信機から離すと33cmごとに顕著な反応が出たといいます。この実験では半波長が33cmだったのだと思われます。つまり波長66cmの電磁波を実験で生じさせたと思われます。

ただし、ヘルツのような方法で測定できる波長は、人間が肉眼で確認できて手で動かせるような程度の波長の大きさの場合だけでしょう。つまり、センチメートル単位や1メートル以上などのような波長です。いっぽう、もし波長がナノメートル単位やマイクロメートル単位などの場合は、回折格子などを使って波長を測定することになります。詳しくは『高等学校物理/物理II/原子と原子核』のコラムを参照せよ。フラウンホーファーやラザフォオードなどの物理学者がスペキュラム合金などの素材を用いて回折格子を作成しています。

磁性体

棒磁石の周りに方位磁針を置いて磁場の向きを調べます。

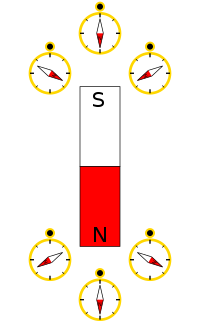
磁石のまわりには別の磁石を動かす力のもととなるものが生じています。 これを磁場（じば、magnetic field）あるいは磁界（じかい）と呼ぶ。（日本の物理学では磁場と呼ぶことが多く、また、日本の電気工学では磁界と呼ばれることが多い。明治期の訳語の際の、日本国内の業界ごとの違いに過ぎず、地域社会的な事象であり、呼び方は物理の本質とは関係ないので、ここでは、どちらの表現を用いるかは、本書では特にこだわりません。英語では物理学・電気工学とも“magnetic field”で共通しています。）

鉄やコバルトやニッケルに磁石を近づけると、磁石に吸い付けられます。 また、鉄やコバルトやニッケルに強い磁化を与えると、鉄やコバルトやニッケルそのものが磁場を周囲に及ぼすようになります。 このような、もともとは磁場を持たなかった物体が、強い磁場を受けたことによって磁場を及ぼすようになる現象を磁化（じか、magnetization）といいます。

あるいは電荷の静電誘導と対応させて、磁化のことを磁気誘導（じきゆうどう、magnetic induction）ともいう。 そして、鉄やコバルトやニッケルのように、磁石に引き付けられ、さらに磁化をする能力がある物体を強磁性体（きょうじせいたい、ferromagnet）といいます。 鉄とコバルトとニッケルは強磁性体です。

銅は磁化しないし、銅は磁石に引きつけられないので、銅は強磁性体ではありません。

磁気遮蔽

静電誘導を利用した、静電遮蔽（せいでんしゃへい）と言われます、中空の導体をつかって物質を囲むことで外部電場を遮蔽する方法があったのと同様の、磁気の遮蔽が、強磁性体でも出来ます。中空の強磁性体を用いて、強磁性体の内部は磁場を遮蔽できます。これを磁気遮蔽（じきしゃへい、magnetic shielding）といいます。磁気シールドともいう。

磁性体：magnetic substance

強磁性体：ferromagnet

常磁性体：paramagnetic substance

反磁性体：diamagnetic snbstance

反磁性体が分かりづらいかもしれませんが、単に、その材料に加えられた磁場を打ち消す方向に、磁化をするだけの材料です。

そもそも、磁力線とあまり相互作用しない物質も多い。たとえば、ガラスや水によます、磁気への影響は、真空の場合とほとんど変わりません。ガラスや水の比透磁率（ひ とうじりつ） μ （ミュー）は、ほぼ1です。

なお、鉄の比透磁率は、状態によって透磁率に数百〜数千の違いがあるが、wikipedia日本語版で調べた場合の鉄の透磁率は約5000です。

では、透磁率がほぼ1の物質は、磁場の方向は、外部磁場を基準として、どちら向きだろうか？ 外部磁場を打ち消す方向に磁化しているのだろうか？ それとも、外部磁場と同じ方向に磁化しているのだろうか？

その違いこそが、常磁性（じょうじせい）と反磁性（はんじせい）のちがい、です。

ある物質が、外部磁場にほとんど反応しませんが、しかし少しだけ外部磁場と同じ方向に、磁化をしている現象のことを常磁性といいです、そのような物質を常磁性体といいます。常磁性体をあらわす物質として、アルミニウムや空気などあります。

いっぽう、ある物質が、外部磁場にほとんど反応しませんが、しかし少しだけ外部磁場を打ち消す方向に、磁化をしている現象のことを反磁性といいです、そのような物質を反磁性体といいます。反磁性体をあらわす物質として、銅や水や水素などなどあります。

※ 範囲外: スピンと磁性体

元素や分子の種類によって、磁性のちがいがある理由として、化学結合での電子軌道に原因があると考えられてます。

化学の教科書の発展事項に、「s軌道」や「p軌道」などの理論があるが、この理論で、その理由を説明できるとされています。なお、答えを先にいうと、「d軌道」の特徴が、磁性の原因です。（証明は省略します。）

もともと、（化学結合で電子殻（でんしかく）に発生することのあります）孤立電子には磁性があり、その磁性が電子が2個そろって（孤立でなくなり）電子対になる事で、磁性が打ち消しあっていると考えられます。なお、孤立電子がもともと持っている磁性のことをスピンといいます。よく化学の理論では、スピンを上矢印「↑」と下矢印「↓」の2種類であらわす事が多いのですが、その理由は、もとをたどれば、そもそも磁石の向きが2種類（たとえばN極とS極という2種類の極があります）だからです。

電子殻とは、化学Iの始めのほうでも習う、「K殻は8個の電子が入る」などの、アレのことです。

まとめると、

• そもそも単独の1個の電子には、じつは磁性があります。そのため、孤立電子には、じつは磁性があります（スピン）。そして、おそらく、この磁性こそが（電子の「スピン」と言われる磁性こそが）、おそらく、孤立電子が電子対になろうとする理由のひとつであり、つまり、おそらく、そもそも共有結合が起きる理由のひとつでしょう。
• しかし、化学反応によって孤立電子は、化学結合として、すぐに周囲の分子や原子と結合してしまうので、孤立電子ではなく電子対になってしまい、2個の反対方向の磁性をもった電子対が、磁性を打ち消しあう。おそらく、このような理由により、多くの（化学結合の結果です）物質は、外部磁場との相互作用が弱い物質が多く、強磁性となる元素や分子の物質は少なく、多くの元素や分子の物質は常磁性または反磁性になってしまうでしょう。

※ 範囲外: 「強誘電体」と圧電体

「磁性体に『強磁性体』があるのなら、誘電体にも『強誘電体』があるのか？」のような疑問は、とうぜん、思うでしょう。

チタン酸鉛 ${\ce {PbTiO3}}$ や、ニオブ酸リチウム ${\ce {LiNbO3}}$ が、「強誘電体」に分類される場合もあります。

しかし、強磁性体が磁気テープや磁気ハードディスクなどの記録メディアに用いられている状況とは異なり、「強誘電体」は記録メディアには用いられていません。過去には、そのような「強誘電体メモリー」を目指す研究開発もあったが、しかし2017年の時点では、まだ「強誘電体メモリー」のようなデバイスは実用化していません。

しかし、他の用途で、これらの物質は産業に実用化されています。

チタン酸鉛やニオブ酸リチウムは、この物質に圧力をくわえると電圧が発生する事から、圧電体（あつでんたい）という素子として活用されています。（※ 『高等学校化学I/セラミックス』で「圧電性セラミックス」として圧電体を紹介。高校化学の範囲内です。2017年の現在では高校3年の選択化学（専門化学）の範囲内でしょう。）

なお、これらの圧電体に、電圧をくわえると、物質がひずむ。

このため、圧電体に交流電圧を加えることで、圧電体が短時間で何回も周期的に振動することにより、圧電体の周囲にある空気も振動させる事ができるので、超音波を発生するための素子として、すでに実用化されています。

なお、ある種類の物質が、圧力をくわえると電圧が発生する現象が起きる物質の場合、そのような性質のことを圧電性（あつでんせい）といいます。

半導体

ケイ素 Si やゲルマニウム Ge は、導体と絶縁体の中間の抵抗率をもつことから、ケイ素（シリコン）やゲルマニウムなどは半導体と言われます。

この半導体の結晶に、わずかに、リンPなどの不純物を入れることで、抵抗率を大きく下げられます。

（※ 範囲外、注釈: ）暗黙の前提すぎるので、検定教科書ではいちいち説明されないかもしれませんが、いわゆる「パソコン」や「コンピュータ」などのハードウェアの内部は、主に半導体からなる部品です。

パソコン部品のうち、いわゆる「メモリ」や、なんなど「チップ」など言われる部分の材料は、たいてい、下記のような意味でのシリコン半導体からなる部品です、

n型半導体

シリコン原子は価電子が4個であり、シリコンの結晶は、4つの価電子が共有結合をしています。

これにリンPが加わると、リンは価電子が5個なので、1個の価電子が余り、この余った価電子が自由電子として、結晶を動き回れるようになります。

このような仕組みで、シリコンにリンを加えることで、抵抗率が大きく低下する、というのが定説です。

このように、負の電子が余ることで、導電率が上がってる半導体を n型半導体 といいます。(「n」は negative の略。)

p型半導体

シリコンの結晶に、不純物として、ホウ素BやアルミニウムAlなど、価電子が3個の元素が加わると、電子が1個、足りなくなります。

この、電子の不足したぶんの空席をホール(postive hole、正孔)といいます。

ホールは正電荷をもちます。

電圧が掛かると、このホールを埋めるように近くの結合にあった電子が移動しますが、もとの電子があった場所に新たなホールができるので、見かけ上はホールが電子と逆方向に動いたように見えます。

よって、ホールが動くことで、電流が流れると見なせます。

また、このように、正の電荷をもつ粒子によって導電率が上がってる半導体を p型半導体 といいます。(「p」は positive の略。)

キャリア

n型半導体では、自由電子が電流を運ぶ。

p型半導体では、ホールが電流を運ぶ。

このように、半導体中で電荷電動の担い手を、キャリア（carrier）といいます。

つまり、n型半導体のキャリアは電子で、p型半導体のキャリアはホールです。

pn接合

ダイオードの順方向。電流は流れます。

ダイオードの逆方向。電流は流れません。

p型半導体とn型半導体を接合し(pn接合)た物体が、一方向のみに電流を流す。

このような部品をダイオード（diode）といいます。

p側に正電圧を掛け、n側に負電圧を掛けた時、電流が流れます。

いっぽう、p側に負電圧を描け、n側に正電圧を掛けても、電流が流れません。

回路において、ダイオードが電流を流す向きを順方向（じゅんほうきましょう）といいます。順方向とは反対向きを逆方向といいます。ダイオードの逆方向には、電流は流れません。

このように一方向に流れる仕組みは、ダイオードでは、つぎのような仕組みで、電流が流れるからです。

このように一方向にだけ電流を流すことを整流（せいりゅう）といいます。なお、半導体を使わなくても、真空管でも整流だけなら可能です。（ただし真空管の場合、熱の発生が膨大であったり、耐久性が劣るので、電子部品としての実用性は、空管は低いので、現代は真空管は電子部品としては使われていません。）

パソコンで、デジタル波形やデジタル信号のように四角の電流波形を作っている方法は、おおむね、このダイオードと、後述するトランジスタとを、うまく組み合わせることで、デジタル波形をつくるという仕組みです。（※ 数研出版の検定教科書も、そういう見解です。）

• p側に正電圧を掛け、n側に負電圧を掛けた時

ダイオードのp側に正電圧をかけ、いっぽうn側に負電圧をかけると、p側では正電極の正電圧からホールが反発して接合面へと向かい、いっぽうn側では自由電子が負電極から反発して接合面へと向かう。そして、接合面で、ホールと自由電子がであい、消滅します。この結果、見掛け上、正電荷が、正電極から負電極に移動したのと、同等の結果になります。

そして、正電極から、つぎつぎとホールが供給されるので、電流が流れ続けます。

• p側に負電圧を描け、n側に正電圧を掛けた時

いっぽう、p側に負電圧を描け、n側に正電圧を掛けた時、p側ではホールは電極（電極には負電圧が掛かってます）に引き寄せられ、接合面からは遠ざかります。同様にn側では自由電子が電極（正電圧が掛かってます）に引き寄せられ、接合面からは遠ざかります。

この結果、接合面には、余分なホールも余分な自由電子もない状態となり、よって接合面の付近にはキャリアがなく、この接合面付近のキャリアの無い部分は空乏層（くうぼうそう、depletion layer）と呼ばれます。

そして、それ以降は、ホールも自由電子も、もうどこにも移動の余地がないので、よって電流が流れません。

※ 範囲外: 「半導体」とは？

物理学や化学でいう半導体とは、上述のように、シリコンなどの結晶および、それらの結晶に、不純物を加えることで電気特性を調整した物質の事です。 いっぽう、磁性体は、半導体ではありません。 しかし、世間一般では、大企業の「半導体メーカー」とされる企業が生産した電子部品が、まとめて「半導体」と言われることもあり、このため、たとえ磁性体を活用した製品であり、半導体をあまり活用していない製品であっても、半導体と言われることも多い。 よくある例としては、磁気ハードディスクですら「半導体」と言われる場合もあります。 しかし、物理学では、磁性体は、けっして半導体ではありません。化学でも同様に、「磁性体は、けっして半導体ではない」として扱う。 磁性体だけでなく、液晶も同様です。 同様に、液晶ディスプレイも、液晶のぶぶんは、半導体ではありません。 大学の物理や化学でも、磁性体は、半導体ではありません、として扱う。液晶も同様であり、大学では、液晶は半導体ではありません、として扱う。 本wikibooks高校教科書でも、磁性体や液晶は、半導体ではありません、として扱う。 なお、中学高校の社会科の地理科目の工業統計では、きちんと「電子部品」という表現で、半導体や液晶、ハードディスクなどを、まとめて表現しています。

トランジスタ

NPN型トランジスタの模式図（バイポーラトランジスタ）

半導体を3つnpnまたはpnpのように組み合わせると、電流を増幅（ぞうふく）することができます。増幅作用（ぞうふくさよう）といいます。

NPNとは、片端から順に見てN型・P型・N型の順に並んでるという事です。

同様に、PNPとは、片端から順に見てN型・P型・N型の順に並んでるという事です。

増幅といっても、けっして無からエネルギーが発生するわけではないので、混同しないように。

説明の簡略化のため、外部電源が省略される事があるが、実際は外部電源も必要です。半導体素子は小さな電流しか流せないので、電流を減らすための抵抗素子としての保護抵抗（ほごていきましょう）も必要です。

なお、図のように長方形状に並んでいる方式のトランジスタをバイポーラトランジスタといいます。（※ 検定教科書の数研出版の教科書で、「バイポーラトランジスタ」をコラムで習う。）

バイポーラトランジスタには、端子が主に3つあり、「エミッタ」や「ベース」や「コレクタ」という合計3つの端子があります。

バイポーラトランジスタでの電流の増幅とは、ベース電流を増幅してコレクタに集めるです（PNPの場合）。電流の向きはPNP型のばあいと NPP型のばあいとでは異なるが、どちらの場合でもベース電流が増幅されるという仕組みは共通です。

さて、模式図では模式的に真ん中の半導体はうすめ、小さめに書かれるが、実際のトランジスタは真ん中の半導体はそうではないので、参考程度に。

教育では、半導体の高校生や専門外（電子専攻以外）の人むけには、よくバイポーラトランジスタが単純なので紹介されるが、実際に市販のコンピュータ部品などでよく使われるトランジスタの方式は、これとは形状がけっこう異なります。

市販のコンピュータ部品のトランジスタには、電界効果トランジスタといわれる方式のものが、よく用いられます。（もちろん、電界効果トランジスタにも、「増幅」の機能があります。）

（※ 啓林館の検定教科書で、「電界効果トランジスタ」がコラム欄で紹介されています。）

※ 電界効果型の場合は、「ソース」や「ゲート」や「ドレイン」などの端子があります。原理は異なるので、対応はしません。

（※ 詳しくは大学の電気工学または工業高校の電子回路などの科目で習う。）

トランジスタは、回路図では、模式的に下図のように書かれます。

NPNトランジスタの図記号。

PNPトランジスタの図記号。

ダイオードやトランジスタの他にも半導体を組み合わせた電子部品はあるのですが（他にも「サイリスタ」など色々とあります）、高校物理の範囲を超えるので、説明は省略します。（※ もし仕事で専門的な情報が必要になれば、工業高校むけの『電子回路』の教科書にけっこう詳しく書いてあるので、それを読めばいいです。なお、書店の資格コーナー本にある電気工事士や電気主任技術者試験などの対策品には、ほぼ電子回路が範囲外なので、あまり電子回路の説明は書いてません。なので、工業高校『電子回路』の教科書、または工業高専などの同等の科目の教科書を参照のこと。）

※ 集積回路について、1990年代くらいの参考書の数研出版チャート式の物理2に、後述のような集積回路などの説明があった。

『情報』教科が2000年代に加わったので、CPUなどの説明の一部が『情報』教科に移動しています。

パソコンのCPUなどの部品も、中身の多くは半導体であり、ダイオードやトランジスタなどの素子がCPUなどの内部にたくさんあります、と言われています。（※ 他にも「水晶振動子」など色々とCPU内には あるが、物理2の範囲外なので説明を省略。）

集積回路やLSI(Large Scale Integrated、大規模集積回路)などと言われる電子部品も、なにを集積（「集積」を英語で integrate インテグレート という）したのかというと、半導体素子を集積したと言う意味です。

なお、「IC」（アイシー）とは Integrated Circuit の略称であり、これを和訳したものが「集積回路」です。

つまり、集積回路やLSIの中身は、半導体であり、トランジスタなどの素子が高密度で、その回路中に詰まっています。

電子部品の半導体の材料としては、通常はシリコン結晶が使われます。（※ 啓林館、数研など、結晶であることも言及。）

研究開発ではシリコン以外の材料も研究されており一部の特殊用途ではGaAsやInGaPなどが利用されているが（※ 数研の検定教科書はGaAsやInGaPなどにコラムで言及）、しかし現状では、シリコンが市販のコンピュータ部品中の半導体素子の材料では主流です。

なお、シリコン半導体の材料内部はシリコン結晶であるが、表面は保護膜および絶縁のために酸化させられており、シリコン半導体表面は酸化シリコンの保護膜になっています。シリコンが酸化すると、絶縁物になるので、保護膜になるわけです（※ 数研出版の教科書もそう言っています。）

半導体の内部に、添加物などで特性を変えることにより、抵抗やコンデンサも半導体内部に製造できます。（※ 数研が、抵抗やコンデンサも半導体内部で作っている事に言及。）

（※ 範囲外: ）しかし、コイルは半導体内部に作ることが出来無いです。

発展： 相対論の一次近似

運動する磁束は電場を誘起する

磁場Bの中を、電荷qの荷電粒子が速度vで運動すると、ローレンツ力はベクトル外積を用いて　f＝q・v×B　の力が粒子に働くが、ここで観測者の座標系を変えたとして、同じ粒子を、粒子と同じ方向に速度ｖで動く座標形Ｋの中の観測者から見たらどうなるか？　座標系Kでは、粒子の速度は v(K)＝0 であり、磁束の速度を V_b とすると、前の座標系の粒子とは反対方向に動くので、

V_b ＝－v です。

新しい座標系Kから観測しても、粒子が f＝q・v×B　の大きさの力を受けて加速されることには変わらませんが、座標系ｋでは、荷電粒子は静止していたのに、ローレンツ力を受けたと考えるのは不合理です。磁束は、V_b＝－v で運動していたので、磁束の運動によって　f＝q・（－V_b）×B ＝ －q・V_b×B　の力を受けたと考えるべきです。粒子を質量0の質点とみなせば、静止している荷電粒子に力を及ぼせるのは、電場だけだから、つまり速度 V_b で運動する磁束が、 E＝－V_b×B の誘導電場を誘起することになります。このとき、磁場と誘導された電場は垂直です。

運動する電場は磁界を作る

もし、「運動する電場は磁界を作る」とすれば、アンペールの法則　「直線状に無限に長い導線を流れる　電流Ｉ　は距離Ｒ　だけ離れた場所に　B・2πr＝μI　の磁場を作ます。」という現象は、じつは「導線の中で荷電粒子が運動することによって、荷電粒子といっしょにその粒子が作る電場も動き、その電場の運動が、磁場を誘起しています。」という可能性があります。 電流が流れている無限長の、まっすぐな導線を考えます。線密度 q[C/m] で分布した電荷は、図のように円筒対称な電荷を作ます。

（※ ここに図を。）

直線から距離ｒのときの電気力線の密度Dは

D＝εE＝ ${\frac {q}{2\pi r}}$

よって

εE・2πr ＝q　　　①

電流 I は電荷分布 q が速度 V_e で運動しているとして　

I ＝ qV_e

[A]＝[c/m]・[m/s]＝[c/m]

と定義すれば、

電流 qV_e が距離 r のところに作る磁場Bはアンペールの法則から、

B・2πr（＝μI）＝ μqV_e　　　②

となります。

このとき、磁場の向きは、V_e から 半径r方向 にねじを回す向きです。

②÷①から B/εE ＝ μ V_e B＝εμ V_e・E

向きまでふくめてベクトル積で表せば、

${\vec {B}}$＝εμ ${\vec {V_{e}}}\times {\vec {E}}$ となります。

つまり

速度 V_e で運動する電場 E は、誘導磁場 B＝εμV_e×E を作ます。

という、重要な結論が得られます。

あるいは、　μH＝B　をもちいて　B＝μH＝εμ V_e ×E　より

H＝εμV_e×E　となって、さらに　D＝εE　より　

H＝μV_e×D　

です。

まとめ

速度 V_bで運動する磁束Bは　

E＝－V_b×B

の誘導電場を誘起します。　　　・・□1

速度 V_e で運動する電場 E は

B ＝ εμ V_e　× E　

の誘導磁場を作ます。

E,Bのかわりに、D,Hを使って表記すれば、

D ＝ －ε V_b × B

かつ

H ＝ V_e × D　　　（・・・□2）　

さて、電磁波が速度Cで真空中を伝わるとすれば、 Vb ＝ Ve ＝ C　とします。 □1式と□2式の外積をとると、

E×H ＝(－V_b×B)× (V_e×D) ＝ (－C×μH) × (C×εE)　

＝　εμ ( C²) E×H

よって

εμ・c² ＝1

です。

よって、電磁波の速度は $c={\frac {1}{\sqrt {\varepsilon \mu }}}$ と予測できます。

このεとμに実測値を入れると、光速の測定値 $c=299792458m/s$ と、高い精度で一致します。

この事から、光は、電磁波である事が分かります。また、電磁波は、光速度Cで真空中を伝わます。

また、これより、運動電場の誘導する磁場は

B ＝ (１/ C² )V_e×E　　　③

とも変形できます。

③式を、ガウスの法則（①式）　と組み合わせると、アンペールの法則（②式）が得られます。 よって、「速度 V_e で運動する電場 E は、　B＝εμ V_e ×E　の誘導磁場を作ます。」という過程が妥当だったことがわかります。

ポインティング ベクトル

電磁波では電場 E と磁場 B が光速 C で運動しているので　磁束の運動速度 V_b は V_b ＝ C であり、誘導電場 E は E ＝－V_b×B であるので、両式より E ＝ －c×B　です。（電磁波の電場と磁場の関係式）なお

$\mathbb {B} =\mu \mathbb {H}$

であるので、 電磁波は

$\mathbb {E} \times \mathbb {H}$

の方向に進んでいるはずです、ということを注目しましょう。

この $\mathbb {E} \times \mathbb {H}$ で定義される量を ポインティング　ベクトル とよぶ。 これは単位面積をとおって流れ出る電磁場のエネルギーの流れの量をあらわす。

さて、電磁場のエネルギー密度は $u={\frac {1}{2}}\varepsilon E^{2}+{\frac {1}{2}}\mu H^{2}$ なので、これに電磁波の電場と磁場の関係式 $\mathbb {E} =-\mathbb {C} \times \mathbb {B}$ を代入して、

$\varepsilon \mu \cdot c^{2}=1$

の関係を用いると、（エネルギーでは、2乗によりマイナス符号がなくなるので、絶対値を取って｜Ｅ｜＝｜ｃ×Ｂ｜　としておくと、計算が簡単になる場合があります。）

結果として　

$u=\varepsilon E^{2}$　　　（電磁波のエネルギー密度）

となります。 電磁波が、壁にあたって吸収されるとき、単位時間に単位面積あたり 光速C の大きさの体積のなかの電磁波が壁に衝突するので、　

c・u　

のエネルギーが、単位時間に単位面積に流れ込むはずです。

ｓ＝ c・u　に u＝ ε・E^2 を代入して、 $\epsilon \mu \cdot c^{2}=1$ と ｜E｜＝｜c×B｜を利用すると、結果的に

　s ＝ ${\frac {1}{\sqrt {\varepsilon \mu }}}\epsilon E^{2}$ ＝${\frac {1}{\sqrt {\varepsilon \mu }}}\epsilon |E||cB|$ ＝｜E｜・｜H｜

です。

よってポインティング　ベクトル E×H は単位面積を通って流れ出る電磁場のエネルギーの流れをあらわす。

E×Hの単位は　[V/m]・[A/m]＝[V・A／m²]＝[W／m²]

ポインティング ベクトル と 運動量密度

ポインティング ベクトル　S ＝ E×H ＝ εμ（C²）E×H は

D＝εE と B＝μH をもちいて S ＝ E×H ＝（C²）D×B とも書けます。

$\mathbb {D} \times \mathbb {B} ={\frac {1}{c^{2}}}\mathbb {E} \times \mathbb {H}$

です。

天下り的な説明ですが、この G＝D×B という量は、運動量の密度です。この量 G＝D×B を、電磁波の「運動量密度」（うんどうりょうみつど）といいます。実際に、D×B の単位は

[D×B] ＝ [｛1 / (C²)｝]　[E×H] ＝ [1 / (ｍ/s)²] [W/m²]

＝ [N・s／m³]

となります。 たしかに、運動量の密度の単位と等しい。

• 発展: 光電効果との関係

ところで、のちの単元で習うが、光電効果では エネルギーuと運動量pの関係は、光速度Cをもちいて、 u＝cp と書けます。

s＝c・u は s＝ cu ＝｜E×H｜ であり、 u＝cp とあわせて、

s＝c (cp) ＝ (c²) p ＝｜E×H｜

これより

p ＝ (1/c²) ｜E×H｜ ＝ εμ ｜E×H｜　

＝ ｜εE×μH｜ ＝ ｜D×B｜

向きまで含めて

p ＝ D×B

となって、確かに G ＝ D×B　は運動量密度となります。

電磁誘導の再検討

長さＬのまっすぐな針金が、速度ｖで磁場Ｂの中を横切るとします。簡単のため、針金の軸と速度ｖの方向と磁場Ｂは垂直とします。このとき、針金の中の電荷にかかる力および電場はローレンツ力により、

F ＝ q v×B

F/q ＝ E ＝ v×B の電位が、針金の長さ方向に派生します。

電場Ｅにそって長さＬだけ、電荷ｑが上げられたら、エネルギーは ｑＥＬ 変化します。電位は Ｖ＝ＥＬ です。

V ＝ LvB ＝ ⊿Φ／⊿t　

これより、誘導電圧 V は、磁束の1秒あたりの時間変化になります。 では、仮に固定された回路の中にソレノイドを通して、このソレノイドに交流電流を流した場合も、回路に誘導電圧が発生するのだろうか。答えは「する」。