放物線(parabola)、楕円(ellipse)、双曲線(hyperbola)をまとめて、2次曲線や円錐曲線という。これらが、2次曲線と呼ばれる理由は、放物線、楕円、双曲線は  の2次式
の2次式  によって
によって  で表すことができ、また
で表すことができ、また  の2次式
の2次式  によって
によって  と表される曲線は放物線、楕円、双曲線、直線、点のいずれかになるからである。
と表される曲線は放物線、楕円、双曲線、直線、点のいずれかになるからである。

円錐曲線と呼ばれる理由は、円錐面を「全ての母線と交わり、底面に平行な平面で切断」したときの断面が円。「全ての母線と交わり、底面に平行でない平面で切断」したときの断面が楕円。「母線に平行な面で切断」したときの断面が放物線。「母線に平行でない平面で切断」したときの断面が双曲線となるからである。
2次曲線は直線や円についで重要な曲線である。
数学Ⅱ「図形と方程式」及び数学C「ベクトル」の先行履修を必須とする。数学C「複素数平面」及び数学Ⅲ「微分法」より前の履修が望ましい。
平面上に点  と、点
と、点  を通らない直線
を通らない直線  をとる。このとき、直線
をとる。このとき、直線  からの距離と点
からの距離と点  からの距離が等しい点の軌跡を放物線(正字:抛物線)という。このとき、点
からの距離が等しい点の軌跡を放物線(正字:抛物線)という。このとき、点  を放物線の焦点、直線
を放物線の焦点、直線  を放物線の準線という。
を放物線の準線という。

焦点を  準線を
準線を  とする放物線の方程式を求める。
とする放物線の方程式を求める。 がこの放物線の点とすると、点
がこの放物線の点とすると、点  と直線
と直線  の距離は
の距離は  であり、
であり、 である。なので、
である。なので、  である。これを整理して、
である。これを整理して、

を得る。
これを放物線の方程式の標準形という。
ここで、放物線  において、
において、  と
と  を入れ替えれば
を入れ替えれば  である。ここから中学から学んできた放物線の定義と一致することがわかる。
である。ここから中学から学んできた放物線の定義と一致することがわかる。
演習問題
放物線  の焦点と準線を求めよ。
の焦点と準線を求めよ。
解答
焦点  準線
準線 
平面上に異なる2点  をとる。
をとる。 との距離と、
との距離と、  との距離の和が一定である点の軌跡を楕円(正字:橢圓)という。このとき、点
との距離の和が一定である点の軌跡を楕円(正字:橢圓)という。このとき、点  を楕円の焦点という。
を楕円の焦点という。
2点F、F'を焦点とする楕円において、直線FF'のうち楕円が切り取る線分を長軸、長軸の垂直二等分線のうち楕円が切り取る部分を短軸という。長軸と短軸の交点を楕円の中心、長軸・短軸それぞれの端点を頂点という。
焦点を  とする。点
とする。点  が楕円上の点であるとき、
が楕円上の点であるとき、  である。
である。 より
より

両辺を2乗して整理すると

再度、両辺を2乗して整理すると

ここで  と置き換えると
と置き換えると

両辺を  で割ると
で割ると

が導かれる。
これを楕円の方程式の標準形という。
x軸との交点は 、
、 、y軸との交点は
、y軸との交点は 、
、 となる。
となる。
 のとき、
のとき、 は長軸の長さ(長径)、
は長軸の長さ(長径)、 は短軸の長さ(短径)となり、xy平面上にグラフを書くと横長の楕円になる。また焦点は長径であるx軸上にありその座標は
は短軸の長さ(短径)となり、xy平面上にグラフを書くと横長の楕円になる。また焦点は長径であるx軸上にありその座標は となる。
となる。
逆に、 のとき、
のとき、 は長軸の長さ(長径)、
は長軸の長さ(長径)、 は短軸の長さ(短径)となり、xy平面上にグラフを書くと縦長の楕円になる。また焦点は長径であるy軸上にありその座標は
は短軸の長さ(短径)となり、xy平面上にグラフを書くと縦長の楕円になる。また焦点は長径であるy軸上にありその座標は となる。
となる。
2つの焦点が近いほど楕円は円に近づき、2つの焦点が重なったとき  となり、楕円は円になる。
となり、楕円は円になる。
楕円と円の関係
楕円 は、
①円
は、
①円 をx軸をもとにy軸方向に
をx軸をもとにy軸方向に 倍したもの。
②円
倍したもの。
②円 をy軸をもとにx軸方向に
をy軸をもとにx軸方向に 倍したもの。
③円
倍したもの。
③円 をx軸方向に
をx軸方向に 倍、y軸方向に
倍、y軸方向に 倍したもの。
倍したもの。
一般に、曲線 をx軸方向に
をx軸方向に 倍、y軸方向に
倍、y軸方向に 倍した曲線の方程式は
倍した曲線の方程式は である。
である。
ちなみに、恒星の周りを公転する惑星の軌道は、恒星を焦点とする楕円になる。
平面上に異なる2点  をとる。
をとる。 との距離と、
との距離と、  との距離の差が一定である点の軌跡を双曲線といい、2点
との距離の差が一定である点の軌跡を双曲線といい、2点  を双曲線の焦点という。
を双曲線の焦点という。
焦点を  とする。点
とする。点  が双曲線上の点であるとき、
が双曲線上の点であるとき、  である。
である。 より
より

両辺を2乗して整理すると

再度両辺を2乗して整理すると

ここで、  とおき、両辺を
とおき、両辺を  で割れば
で割れば

である。
これを、双曲線の方程式の標準形という。
なお、双曲線 を単位双曲線という場合がある。
を単位双曲線という場合がある。
双曲線が で表されるとき、焦点の座標は
で表されるとき、焦点の座標は となる。
となる。
逆に、双曲線が で表されるとき、焦点の座標は
で表されるとき、焦点の座標は となる。
となる。
双曲線 は2本の漸近線
は2本の漸近線 を持つ。
を持つ。
漸近線が直交する双曲線を直角双曲線という。
一般に、曲線 をx軸方向にp、y軸方向にqだけ平行移動して得られる図形の方程式は、
をx軸方向にp、y軸方向にqだけ平行移動して得られる図形の方程式は、

である。
この事実を利用して、2次式 が表す図形を判別しよう。
が表す図形を判別しよう。
方程式 が表す図形を答えよ。
が表す図形を答えよ。
yについて平方完成すると なので
なので 。これは放物線
。これは放物線 をx軸方向に-4、y軸方向に3だけ平行移動した図形である。
をx軸方向に-4、y軸方向に3だけ平行移動した図形である。
- 問題
- 以下の方程式が表す図形を答え、その概形を書け。



複素数平面の知識を用いると、二次曲線の回転移動について考えることができる。
詳細な解説はあちらのページに載っているので割愛するが、曲線 を原点を中心に
を原点を中心に だけ回転した図形の方程式は
だけ回転した図形の方程式は である。
である。
分数関数 について考える。この関数のグラフは「反比例のグラフ」という名前で中学校で学んだ。関数の式を変形すると、
について考える。この関数のグラフは「反比例のグラフ」という名前で中学校で学んだ。関数の式を変形すると、 となる。これを原点を中心に
となる。これを原点を中心に だけ回転してみよう。
だけ回転してみよう。
回転した図形の方程式は である。
である。 より、
より、 なので、
なので、 である。
である。
つまり、関数 のグラフは双曲線
のグラフは双曲線 を原点を中心に回転移動した図形である。この図形の漸近線はx軸とy軸であり、これらの座標軸は直交するので、分数関数
を原点を中心に回転移動した図形である。この図形の漸近線はx軸とy軸であり、これらの座標軸は直交するので、分数関数 のグラフは直角双曲線である。
のグラフは直角双曲線である。
このことから、一次分数関数 のグラフは全て直角双曲線であることがわかる。
のグラフは全て直角双曲線であることがわかる。
なお、回転移動には行列の知識を用いても良い。
点・関数のグラフの移動の総纏め
| 移動の種類 |
点 が移る点 が移る点 |
曲線 が移る曲線の方程式 が移る曲線の方程式 |
備考
|
① 軸方向に 軸方向に 、 、 軸方向に 軸方向に だけ平行移動 だけ平行移動 |
 |
 |
|
② 軸に関する対称移動 軸に関する対称移動 |
 |
 |
|
③ 軸に関する対称移動 軸に関する対称移動 |
 |
 |
|
| ④原点に関する対称移動 |
 |
 |
|
⑤直線 に関する対称移動 に関する対称移動 |
 |
 |
移った関数は元の関数の逆関数である。
|
⑥直線 に関する対称移動 に関する対称移動 |
 |
 |
④と⑤を合成したもの。
|
⑦直線 に関する対称移動 に関する対称移動 |
 |
 |
|
⑧直線 に関する対称移動 に関する対称移動 |
 |
 |
|
⑨点 に関する対称移動 に関する対称移動 |
 |
 |
⑦と⑧を合成したもの。
|
⑩原点を中心とした角 の回転移動 の回転移動 |
 |
 |
|
⑪原点を中心とした 方向 方向 倍、y方向 倍、y方向 倍の拡大・縮小(相似変換) 倍の拡大・縮小(相似変換) |
 |
 |
|
証明は非常に容易であるが、グラフの移動について以下のような考え方を用いている。
- 曲線上の任意の点
 が移った先の点を
が移った先の点を とおく。このとき、「移動と逆の操作をすると点
とおく。このとき、「移動と逆の操作をすると点 が点
が点 に移る」と考えることで、
に移る」と考えることで、 という関係式が出てくる。あとは
という関係式が出てくる。あとは を計算すれば移動した曲線の方程式が出てくる。
を計算すれば移動した曲線の方程式が出てくる。
この考え方は、この分野を含む軌跡の問題で非常に重要な考え方である。
二次曲線と直線の交点は、それぞれの方程式を連立させた連立方程式の実数解として得られる。特に、1文字を消去して得られる二次方程式が重解を持つ場合、直線はその二次曲線の接線である。
与えられた直線が二次曲線の接線であることを示す場合、方程式を連立させて出てくる二次方程式の解が重解であることを示せば良い。数学Ⅲで習う陰関数微分を知っている場合は、微分で接線を求めて与えられた直線に一致することを示すのが最も楽である。
円の接線(復習)
円 上の点
上の点 における接線の方程式は、
における接線の方程式は、

二次方程式の重解を利用した証明は数学Ⅱで既に扱ったため、ここでは正射影ベクトルを用いた証明を紹介する。
- 円の中心を
 、接点を
、接点を 、接線上の任意の点を
、接線上の任意の点を とおく。
とおく。
- 円の半径と接線は常に垂直であるので、
 の正射影ベクトルは常に
の正射影ベクトルは常に と一致する。
と一致する。
- よって
 が常に成り立つ。
が常に成り立つ。
- 成分表示すると、
 が得られる。
が得られる。
- 逆に、上式を満たす点
 は接線上にある。
は接線上にある。
この証明は高校範囲における円の接線の方程式の導出の中で最も簡潔なものである。
なお、偏微分の知識が必要だが法線ベクトルを用いたより簡潔な証明も存在する。
放物線の接線
放物線 上の点
上の点 における接線の方程式は、
における接線の方程式は、

- この放物線の接線はx軸に平行でないから、求める接線の方程式は
 ・・・①と表せる。
・・・①と表せる。
- xを消去して整理すると、

- これが重解を持つから、





- ①に代入して、




なお、放物線 について、接線の方程式はxとyをそれぞれ入れ替えた式となる。
について、接線の方程式はxとyをそれぞれ入れ替えた式となる。
楕円・双曲線の接線
楕円 上の点
上の点 における接線の方程式は、
における接線の方程式は、
 双曲線
双曲線 上の点
上の点 における接線の方程式は、
における接線の方程式は、
 (複合同順)
(複合同順)
- 放物線・双曲線の式を
 とおく。(
とおく。( で楕円、
で楕円、 (複合同順)で双曲線)
(複合同順)で双曲線)
 のときを考える。
のときを考える。- 求める接線の方程式を
 ・・・②とおく。
・・・②とおく。
- yを消去すると


- 点
 における接線が存在するのでこの方程式は
における接線が存在するのでこの方程式は を重解に持つ。
を重解に持つ。
- よって二次方程式の重解の公式より、




- ②に代入して


- ここで点
 が曲線上の点であることから
が曲線上の点であることから が成り立つので、
が成り立つので、 である。
である。
 のとき、
のとき、 から接線の式は
から接線の式は なので成り立つ。
なので成り立つ。
なお、楕円の接線の方程式については次のように証明することもできる。
- 楕円
 をy軸方向に
をy軸方向に 倍すると、楕円は円
倍すると、楕円は円 へ、楕円上の点
へ、楕円上の点 は円上の点
は円上の点 へと写る。
へと写る。
- この点における円の接線の方程式は
 である。
である。
- 逆に円をy軸方向に
 倍すると、この接線は直線
倍すると、この接線は直線 へと写る。
へと写る。
- この直線は楕円上の点
 における接線であり、方程式を変形すると、
における接線であり、方程式を変形すると、 となる。
となる。
一般の点のまわりで考える場合については、先ほど紹介した平行移動の公式を用いれば良い。
後述するが、二次曲線の接線には焦点に関わる美しい性質がある。
放物線と同様に、楕円や双曲線も焦点と準線をもとに定義することができる。
座標平面上に定点F と定直線
と定直線 をとる。点P
をとる。点P からLに下ろした垂線の足をHとし、
からLに下ろした垂線の足をHとし、 とおく。(
とおく。( はイプシロンと読むギリシャ文字)
はイプシロンと読むギリシャ文字)
このとき、


両辺を二乗して整理すると、

① のとき
のとき

- この曲線とF、Lをそれぞれx軸方向に
 だけ平行移動して
だけ平行移動して とおくと、
とおくと、

- これは放物線である。
② のとき
のとき

- 平方完成して、


- この曲線とF、Lをそれぞれx軸方向に
 だけ平行移動して、
だけ平行移動して、

- (Ⅰ)
 のとき
のとき
 とおくと、
とおくと、
- これは楕円である。
- このとき、

- (Ⅱ)
 のとき
のとき
 とおくと、
とおくと、
- これは双曲線である。
- このとき、

なお、準線は焦点1つにつき1本定まるので、楕円・双曲線の準線は2本存在する。
このように、定点F(焦点)からの距離とFを通らない定直線L(準線)からの距離の比がε:1である点Pの軌跡はεの値によって定まる。このεのことを離心率という。
離心率は全ての正の実数値をとりうる。
離心率の値を少しづつ変化させた場合の軌跡を描いていくと、εが0に近づけば近づくほど真円に、εが∞に近づけば近づくほど直線に近い形状になることがわかる。
このことから、離心率による二次曲線の分類は以下のようになる。
離心率と二次曲線
①ε=0のとき
Fを中心とする真円
②0<ε<1のとき
Fを焦点の一つとする楕円
③ε=1のとき
Fを焦点、Lを準線とする放物線
④ε>1のとき
Fを焦点の一つとする双曲線
⑤ε→∞のとき
Fに限りなく近い点を通る直線
離心率はよく「二次曲線が真円から離れている度合い」と表現される。
なお、地球を楕円と見たときの離心率はε ≒ 0.081819191042815790である。
0<ε<1のとき、ε² = f(2-f)となるfは「円に対して楕円がどのくらい潰れているかの度合い」を表し、扁平率(へんぺいりつ)と呼ばれる。
二次曲線が円錐の切り口であるという話を冒頭でしたが、このとき準線と焦点がどこにあるのか紹介しよう。
- 円錐をその頂点を通らない平面で切った切り口は二次曲線である。
- 円錐に内接して切り口にも接する球を考えると、球と平面の接点が二次曲線の焦点となる。
- 球と円錐が接する点でできる円を含む平面と切り口の平面との交線が二次曲線の準線となる。
「焦点」という名前の由来は、以下の性質である。
二次曲線の反射定理
放物線の軸に平行に進む光線は、放物線に当たって反射すると全て焦点に集まる。
楕円の焦点から発した光線は、楕円に当たって反射すると全てもう一方の焦点に集まる。
双曲線の焦点に向かって進む光線は、双曲線に当たって反射すると全てもう一方の焦点に集まる。
- 放物線
 上の点
上の点 における接線とx軸との交点をQ、放物線の焦点をFとおく。
における接線とx軸との交点をQ、放物線の焦点をFとおく。
- 定義よりFの座標は
 。
。
- 接線の方程式は
 なので、Qの座標は
なので、Qの座標は である。
である。
- したがって

- また、

- よって
 が成り立つので
が成り立つので は二等辺三角形であり、
は二等辺三角形であり、 が成り立つ。
が成り立つ。
- この性質から、放物線の軸に平行に進む光線は放物線に当たって反射すると全て焦点に集まることがわかる。
- 楕円
 の2つの焦点をF、F'とする。座標軸上にない楕円上の点
の2つの焦点をF、F'とする。座標軸上にない楕円上の点 における接線とx軸、y軸との交点をそれぞれQ、Rとおく。また、焦点のx座標の絶対値をc、離心率を
における接線とx軸、y軸との交点をそれぞれQ、Rとおく。また、焦点のx座標の絶対値をc、離心率を とする。
とする。
- 接線の方程式は
 なので、Qの座標は
なので、Qの座標は である。
である。
- したがって、

- また、

- さらに、

- 同様にして、

- よって、
 より線分
より線分 は
は の外角を二等分するので、
の外角を二等分するので、
- Pが座標軸上にある場合も、明らかに成り立つ。
- この性質から、楕円の一方の焦点から走った光線は楕円に当たって反射すると全て他の焦点に集まることがわかる。
双曲線の場合も楕円と全く同様の証明である。
補:二変数二次方程式の表す図形が円錐曲線にならない場合
[編集]二変数二次方程式 の表す図形が必ず放物線・楕円・双曲線のいずれかになるわけではない。
の表す図形が必ず放物線・楕円・双曲線のいずれかになるわけではない。
例えば、 と因数分解できる場合、この方程式が表す図形は交わる2直線
と因数分解できる場合、この方程式が表す図形は交わる2直線 である。
である。
また、 と因数分解できる場合、この方程式が表す図形は直線
と因数分解できる場合、この方程式が表す図形は直線 である。
である。
他にも、 と変形できる場合、この方程式が表す図形は点
と変形できる場合、この方程式が表す図形は点 である。
である。
図形が平面上に存在しない場合もある。
例えば、 の表す図形は、xとyが実数の場合xy平面上に描画できない。xとyが複素数である場合を考えると、xy空間(
の表す図形は、xとyが実数の場合xy平面上に描画できない。xとyが複素数である場合を考えると、xy空間( とおいたときにa軸, b軸, c軸, d軸がなす四次元の直交座標空間)のうち実軸同士がつくる平面とは交わらない部分に図形が存在する。この図形は楕円と方程式が似ているので虚楕円と呼ばれる。
とおいたときにa軸, b軸, c軸, d軸がなす四次元の直交座標空間)のうち実軸同士がつくる平面とは交わらない部分に図形が存在する。この図形は楕円と方程式が似ているので虚楕円と呼ばれる。
数学Ⅱで習った虚円も、方程式の表す図形が実数平面と交わらないだけで、x,yを複素数範囲に広げて四次元空間を考えると図形を描画することができる。
このような特殊な場合を除くと、二次曲線の判別式を考えることができる。詳しくは理数科向けのページで扱う。
ベクトルにおいて、点 を通り方向ベクトル
を通り方向ベクトル に平行な直線の方程式は媒介変数(パラメータ)
に平行な直線の方程式は媒介変数(パラメータ) を用いて
を用いて と表せ、このような表示法を媒介変数表示(パラメータ表示)と呼ぶことを学んだ。
と表せ、このような表示法を媒介変数表示(パラメータ表示)と呼ぶことを学んだ。
一般に、媒介変数tを用いて と表される点
と表される点  の集合は曲線を描く。ここでは、曲線の媒介変数表示について扱う。
の集合は曲線を描く。ここでは、曲線の媒介変数表示について扱う。
 サイクロイド
サイクロイド
媒介変数表示では  の形では表しにくい曲線も簡潔に表すことができる。例えば、
の形では表しにくい曲線も簡潔に表すことができる。例えば、
 である。これはサイクロイドと呼ばれる。(一番最後の節により詳細を記した。)
である。これはサイクロイドと呼ばれる。(一番最後の節により詳細を記した。)
一般に、 と媒介変数表示されている曲線を
と媒介変数表示されている曲線を  方向に
方向に  、
、  方向に
方向に  だけだけ平行移動した曲線は
だけだけ平行移動した曲線は  と表せる。
と表せる。
 で表される曲線は
で表される曲線は  を消去すると
を消去すると  となるので放物線である。
となるので放物線である。
円  を媒介変数表示すると
を媒介変数表示すると  となる。これは三角関数の定義より明らかである。このことから、三角関数のことを円関数と呼ぶ場合もある。
となる。これは三角関数の定義より明らかである。このことから、三角関数のことを円関数と呼ぶ場合もある。
楕円 を媒介変数表示すると
を媒介変数表示すると となる。これは円の媒介変数表示と先ほど紹介した拡大・縮小の公式から容易に導出できる。
となる。これは円の媒介変数表示と先ほど紹介した拡大・縮小の公式から容易に導出できる。
双曲線 の媒介変数表示は
の媒介変数表示は となる。これは三角関数の公式
となる。これは三角関数の公式 からわかる。
からわかる。
双曲線関数
ネイピア数 を用いて
を用いて と定義すると、
と定義すると、 が成り立つので、上記の双曲線の式は
が成り立つので、上記の双曲線の式は と媒介変数表示できる。
と媒介変数表示できる。
 と定めると、
と定めると、 (シャイン、コッシュ、タンチもしくはハイパボリックサイン、ハイパボリックコサイン、ハイパボリックタンジェントと読む)は三角関数と似た公式(相互関係、加法定理、微積分公式など)が幾つも成り立つ。そこで、この3つの関数とその逆数を纏めて双曲線関数と呼ぶことにする。
(シャイン、コッシュ、タンチもしくはハイパボリックサイン、ハイパボリックコサイン、ハイパボリックタンジェントと読む)は三角関数と似た公式(相互関係、加法定理、微積分公式など)が幾つも成り立つ。そこで、この3つの関数とその逆数を纏めて双曲線関数と呼ぶことにする。
逆三角関数と並び、双曲線関数とその逆関数は大学入試においてある種の定積分の問題を解く際に役立つことで有名である。その問題はこれらの関数の微積分公式を背景としているため、これらの関数で置換すると簡単に解けるようになっている。
 のグラフは懸垂線(カテナリー)と呼ばれる有名な曲線を描くことで知られている。
のグラフは懸垂線(カテナリー)と呼ばれる有名な曲線を描くことで知られている。
三角関数(円関数)と双曲線関数は非常に似た性質を持つが、これは双曲線関数の定義式が三角関数の複素指数関数表示を実数範囲で書き換えたものであり、更には両者とも第一種不完全楕円積分の逆関数で定義される(ヤコビの)楕円関数の特別な場合を指しているからである。
なお、(複素数 の方程式)
の方程式) の形で表された式を
の形で表された式を の極形式を用いて解くと二次曲線の媒介変数表示が現れる場合がある。
の極形式を用いて解くと二次曲線の媒介変数表示が現れる場合がある。
これまでの学習では、 軸と
軸と 軸を使った座標平面(直交座標という)
軸を使った座標平面(直交座標という) 使うことで、座標平面上の1点を定めた。
ここで学ぶ極座標では、
使うことで、座標平面上の1点を定めた。
ここで学ぶ極座標では、 の文字で与えられる式を使って曲線を表すことを考える。
の文字で与えられる式を使って曲線を表すことを考える。
ある一点Oと半直線OXを定めると、平面上の点Pは、点Oからの距離rと、 XOPの角
XOPの角 の大きさで一意に定まる。
の大きさで一意に定まる。
- 極座標の定義
原点Oと軸OXを定める。平面上の点Pについて、OP間の距離をr、 XOPの大きさをθで表した座標
XOPの大きさをθで表した座標 を極座標という。
このとき、Oを極、OXを始線という。
また、
を極座標という。
このとき、Oを極、OXを始線という。
また、 を偏角という。
を偏角という。
また、直交座標と極座標の関係は次のようになる。
- 直交座標と極座標の関係

これは、原点中心, 半径rの円周上における正弦関数・余弦関数の定義そのものである。
r=0の場合、正弦・余弦の値が存在しないので偏角θを定められない。
そのため、θを任意の実数とすると極座標(0, θ)は極Oを表す。
極座標(r, θ)で定められる平面をrθ平面もしくは極座標平面という。
θを不定にすると点(r, θ)の軌跡は円となる。そのため、二次元における極座標を円座標という場合がある。
物理学や工学方面に進学すると、三次元における極座標を用いるようになる。特に、解析力学や姿勢制御で使われている。
 (陽関数表示)あるいは
(陽関数表示)あるいは (陰関数表示)の形で与えられる式を極方程式(きょくほうていしき)という。極方程式はrとθについての関数であるが、これらはxとyへの変換が可能であり、よってxy平面上に曲線をかいてもよいことになる。
(陰関数表示)の形で与えられる式を極方程式(きょくほうていしき)という。極方程式はrとθについての関数であるが、これらはxとyへの変換が可能であり、よってxy平面上に曲線をかいてもよいことになる。
極方程式においては、rが負の場合も考える。rを正とするとき、(-r, θ)という点は(r, θ+π)と書き換えられる。これは三角関数のθ+πの公式から明らかである。この点は点(r, θ)と極Oに関して対象である。単に極座標の場合は考えない。あくまでも、極方程式を考える場合のみである。同様に、三角関数や複素数平面の場合も考えない。
- さまざまな極方程式
(1)中心O,半径aの円 
(2)中心 ,半径aの円
,半径aの円 
(3)極Oを通り、始線とαの角をなす直線 
(4)点 を通り、OAに垂直な直線
を通り、OAに垂直な直線 
(例)円 を極方程式で表す.
を極方程式で表す.
 を代入して整理すると
を代入して整理すると

 は極を表すから
は極を表すから 
一般に、二次曲線は離心率を用いた極方程式 で表される。
で表される。
離心率の値による2次曲線の分類は直交座標でも極座標でも変化しない。
これまでに、2次曲線、媒介変数表示、極方程式などの曲線とその性質について述べてきた。以下では、これらを利用してさまざまな曲線の式を示す。一般に概形をつかむのは困難なため、コンピュータを使用する。媒介変数表示されている場合は、媒介変数微分を用いることで概形を描ける場合がある。
 サイクロイドの回転円による描画
サイクロイドの回転円による描画
関数表示:
任意の2点間を結ぶ曲線のうち、重力のみが作用する環境下で曲線上を滑らかに動く物体が初速度0で位置エネルギー最大の地点から最小の地点まで動く際に最も速度が大きくなるようなものを最速降下曲線という。
最速降下曲線はサイクロイドの一種であることが証明されている。
 a=1の場合のカージオイド
a=1の場合のカージオイド
関数表示:
カップに入ったミルクティーに光が当たるとカージオイドのような図形が見えることがある。
これは、カージオイドの半円部分で反射した光が一点には集まらないものの、密集するためである。
 アステロイドの内接円による描画
アステロイドの内接円による描画
関数表示:
アステロイドは4つの尖点を持つので、四尖点形ともいう。
中心 で半径
で半径 の定円
の定円 上を半径
上を半径 の円
の円 が内接しながら滑ることなく回転するとき、円
が内接しながら滑ることなく回転するとき、円 上の定点
上の定点 の初期座標を
の初期座標を とすると
とすると の軌跡はアステロイドとなる。
の軌跡はアステロイドとなる。
 リマソン
リマソン
関数表示:
x軸に関して線対称である。
 のときカージオイドに一致する。
のときカージオイドに一致する。
 薔薇曲線r=sin(n/d×θ)
薔薇曲線r=sin(n/d×θ)
関数表示:
nの値を有理数範囲で変えていくと、非常に多彩な図形が現れる。特に、nの値が整数のときは植物の葉のように見える。
このことから、正葉曲線という別名が存在する。
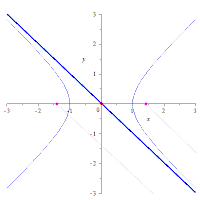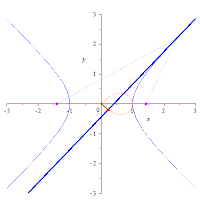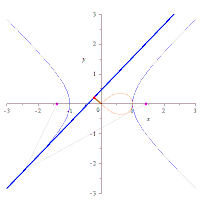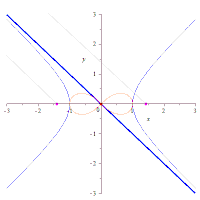 レムニスケートの直角双曲線による描画
レムニスケートの直角双曲線による描画
関数表示:
「∞」に似た図形となる。
ループ一つで囲まれた領域の面積は である。
である。
直角双曲線の接線に、原点から垂線を下ろした点の軌跡はレムニスケートになる。
 リサージュ曲線x=Asin(at)∧y=Bsin(bt+δ)
リサージュ曲線x=Asin(at)∧y=Bsin(bt+δ)
関数表示: (ただし、p, qは有理数)
(ただし、p, qは有理数)
リサジュー曲線とも呼ばれる。
互いに直交する二つの単振動を合成して得られる平面図形はリサージュとなる。
オシロスコープを用いて定数の値を少しづつ変えていくと、図形の多彩で細やかな変化を観察できる。
 アルキメデスの螺旋
アルキメデスの螺旋
関数表示: (ただしa>0, θ≧0)
(ただしa>0, θ≧0)
各線同士の間隔は等しい。
θを負の値にするとy軸に関して線対称となる。
他に代数螺旋と呼ばれている曲線としては、抛物螺旋( )、双曲螺旋(
)、双曲螺旋( )、リチュース(
)、リチュース( )がある。
)がある。
これらの曲線を表す極方程式を について解くと、
について解くと、
- アルキメデスの螺旋:

- 抛物螺旋:

- 双曲螺旋:

- リチュース:

となる。































































































































































































































































































