ここでは、数学IIの微分・積分の考え で学んだ積分の性質についてより詳しく扱う。また、三角関数や指数・対数関数などの関数の積分についても学習する。
高等学校数学 の全ての分野を学んだ後に学習に取り組んでほしい。
積分法について
∫
{
f
(
x
)
+
g
(
x
)
}
d
x
=
∫
f
(
x
)
d
x
+
∫
g
(
x
)
d
x
,
{\displaystyle \int \{f(x)+g(x)\}dx=\int f(x)dx+\int g(x)dx,}
∫
a
f
(
x
)
d
x
=
a
∫
f
(
x
)
d
x
{\displaystyle \int af(x)dx=a\int f(x)dx}
が成り立つ。
∫
{
f
(
x
)
+
g
(
x
)
}
d
x
=
∫
f
(
x
)
d
x
+
∫
g
(
x
)
d
x
{\displaystyle \int \{f(x)+g(x)\}dx=\int f(x)dx+\int g(x)dx}
の両辺を微分すると、
左辺 =右辺 =
f
+
g
{\displaystyle f+g}
が従う。
よって、
∫
{
f
(
x
)
+
g
(
x
)
}
d
x
=
∫
f
(
x
)
d
x
+
∫
g
(
x
)
d
x
{\displaystyle \int \{f(x)+g(x)\}dx=\int f(x)dx+\int g(x)dx}
の両辺は一致する。
(実際には2つの関数の導関数が一致するとき、
それらの関数には定数だけのちがいがある。
仮に、F(x)とG(x)が共通の導関数h(x)を持ったとする。
このとき、
(
F
(
x
)
−
G
(
x
)
)
′
=
h
(
x
)
−
h
(
x
)
=
0
{\displaystyle (F(x)-G(x))'=h(x)-h(x)=0}
となるが、0の原始関数は定数Cであることが分かる。
よって、両辺を積分すると、
F
(
x
)
−
G
(
x
)
=
C
{\displaystyle F(x)-G(x)=C}
となり、F(x)とG(x)には定数だけの差しかないことが確かめられた。
よって、
∫
{
f
(
x
)
+
g
(
x
)
}
d
x
=
∫
f
(
x
)
d
x
+
∫
g
(
x
)
d
x
{\displaystyle \int \{f(x)+g(x)\}dx=\int f(x)dx+\int g(x)dx}
は定数だけのちがいを含んで成り立つ式である。
より一般に、不定積分が絡む等式は定数分の差を含めて成り立つというのが通例である。)
∫
a
f
(
x
)
d
x
=
a
∫
f
(
x
)
d
x
{\displaystyle \int af(x)dx=a\int f(x)dx}
についても両辺を微分すると、
左辺=右辺= a f(x)
が従う。
よって、
∫
a
f
d
x
=
a
∫
f
d
x
{\displaystyle \int afdx=a\int fdx}
が成り立つことが分る。
f
(
x
)
{\displaystyle f(x)}
F
(
x
)
{\displaystyle F(x)}
∫
a
b
f
(
x
)
=
F
(
b
)
−
F
(
a
)
=
−
(
F
(
a
)
−
F
(
b
)
)
=
−
∫
b
a
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,=F(b)-F(a)=-(F(a)-F(b))=-\int _{b}^{a}f(x)\,dx}
∫
a
c
f
(
x
)
d
x
+
∫
c
b
f
(
x
)
d
x
=
(
F
(
c
)
−
F
(
a
)
)
+
(
F
(
b
)
−
F
(
c
)
)
=
F
(
b
)
−
F
(
a
)
=
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx=(F(c)-F(a))+(F(b)-F(c))=F(b)-F(a)=\int _{a}^{b}f(x)\,dx}
関数の原始関数を求める手段として、
積分変数を別の変数で置き換えて積分を行なう手段が知られている。
これを置換積分と呼ぶ。
∫
f
(
g
(
x
)
)
d
g
(
x
)
=
∫
f
(
g
(
x
)
)
g
′
(
x
)
d
x
{\displaystyle \int f(g(x))dg(x)=\int f(g(x))g'(x)dx}
∫
f
(
g
(
x
)
)
d
g
(
x
)
=
F
(
g
(
x
)
)
{\displaystyle \int f(g(x))dg(x)=F(g(x))}
x
{\displaystyle x}
F
′
(
g
(
x
)
)
=
f
(
g
(
x
)
)
g
′
(
x
)
{\displaystyle F'(g(x))=f(g(x))g'(x)}
再び
x
{\displaystyle x}
∫
f
(
g
(
x
)
)
d
g
(
x
)
=
∫
f
(
g
(
x
)
)
g
′
(
x
)
d
x
{\displaystyle \int f(g(x))dg(x)=\int f(g(x))g'(x)dx}
∫
f
(
a
x
+
b
)
d
x
=
1
a
∫
f
(
a
x
+
b
)
d
(
a
x
+
b
)
{\displaystyle \int f(ax+b)dx={\frac {1}{a}}\int f(ax+b)d(ax+b)}
∫
{
f
(
x
)
}
n
f
′
(
x
)
d
x
=
1
n
+
1
{
f
(
x
)
}
n
+
1
+
C
(
n
≠
−
1
)
{\displaystyle \int \{f(x)\}^{n}f'(x)dx={\frac {1}{n+1}}\{f(x)\}^{n+1}+C(n\neq -1)}
∫
f
′
(
x
)
f
(
x
)
d
x
=
log
|
f
(
x
)
|
+
C
{\displaystyle \int {\frac {f'(x)}{f(x)}}dx=\log |f(x)|+C}
∫
(
a
x
+
b
)
2
d
x
{\displaystyle \int (ax+b)^{2}dx}
t
=
a
x
+
b
{\displaystyle t=ax+b}
この両辺を微分すると
d
t
=
a
d
x
{\displaystyle dt=adx}
∫
t
2
d
t
a
{\displaystyle \int t^{2}{\frac {dt}{a}}}
=
t
3
3
a
+
C
{\displaystyle ={\frac {t^{3}}{3a}}+C}
=
(
a
x
+
b
)
3
3
a
+
C
{\displaystyle ={\frac {(ax+b)^{3}}{3a}}+C}
となることがわかる。
実際この式をxで微分すると
(
a
x
+
b
)
2
{\displaystyle (ax+b)^{2}}
置換積分を使わずに計算することも出来る。
∫
(
a
x
+
b
)
2
d
x
{\displaystyle \int (ax+b)^{2}dx}
=
∫
(
a
2
x
2
+
2
a
b
x
+
b
2
)
d
x
{\displaystyle =\int (a^{2}x^{2}+2abx+b^{2})dx}
=
a
2
3
x
3
+
a
b
x
2
+
b
2
x
+
C
′
{\displaystyle ={\frac {a^{2}}{3}}x^{3}+abx^{2}+b^{2}x+C'}
=
a
2
3
x
3
+
a
b
x
2
+
b
2
x
+
b
3
3
a
+
C
{\displaystyle ={\frac {a^{2}}{3}}x^{3}+abx^{2}+b^{2}x+{\frac {b^{3}}{3a}}+C}
(
C
′
=
b
3
3
a
+
C
{\displaystyle C'={\frac {b^{3}}{3a}}+C}
=
(
a
x
+
b
)
3
3
a
+
C
{\displaystyle ={\frac {(ax+b)^{3}}{3a}}+C}
関数の積の積分を行なうときある関数の微分だけを取りだして積分すると、うまく積分できる場合がある。関数
g
(
x
)
{\displaystyle g(x)}
G
(
x
)
{\displaystyle G(x)}
∫
f
(
x
)
g
(
x
)
d
x
=
f
(
x
)
G
(
x
)
−
∫
f
′
(
x
)
G
(
x
)
d
x
{\displaystyle \int f(x)g(x)\,dx=f(x)G(x)-\int f'(x)G(x)\,dx}
積の微分法より
{
f
(
x
)
G
(
x
)
}
′
=
f
′
(
x
)
G
(
x
)
+
f
(
x
)
g
(
x
)
{\displaystyle \{f(x)G(x)\}'=f'(x)G(x)+f(x)g(x)}
f
(
x
)
g
(
x
)
=
{
f
(
x
)
G
(
x
)
}
′
−
f
′
(
x
)
G
(
x
)
{\displaystyle f(x)g(x)=\{f(x)G(x)\}'-f'(x)G(x)}
である。両辺をxで積分して
∫
f
(
x
)
g
(
x
)
d
x
=
f
(
x
)
G
(
x
)
−
∫
f
′
(
x
)
G
(
x
)
d
x
{\displaystyle \int f(x)g(x)\,dx=f(x)G(x)-\int f'(x)G(x)\,dx}
が得られる。
例えば、
∫
x
(
a
x
+
b
)
3
d
x
{\displaystyle \int x(ax+b)^{3}dx}
=
∫
x
(
(
a
x
+
b
)
4
4
a
)
′
d
x
{\displaystyle =\int x\left({\frac {(ax+b)^{4}}{4a}}\right)'dx}
=
x
(
(
a
x
+
b
)
4
4
a
)
−
∫
(
x
)
′
(
a
x
+
b
)
4
4
a
d
x
{\displaystyle =x\left({\frac {(ax+b)^{4}}{4a}}\right)-\int (x)'{\frac {(ax+b)^{4}}{4a}}dx}
=
x
(
(
a
x
+
b
)
4
4
a
)
−
∫
(
x
)
′
(
a
x
+
b
)
4
4
a
d
x
{\displaystyle =x\left({\frac {(ax+b)^{4}}{4a}}\right)-\int (x)'{\frac {(ax+b)^{4}}{4a}}dx}
=
x
(
(
a
x
+
b
)
4
4
a
)
−
∫
(
a
x
+
b
)
4
4
a
d
x
{\displaystyle =x\left({\frac {(ax+b)^{4}}{4a}}\right)-\int {\frac {(ax+b)^{4}}{4a}}dx}
=
x
(
(
a
x
+
b
)
4
4
a
)
−
(
a
x
+
b
)
5
20
a
2
{\displaystyle =x\left({\frac {(ax+b)^{4}}{4a}}\right)-{\frac {(ax+b)^{5}}{20a^{2}}}}
部分積分を
n
{\displaystyle n}
∫
f
(
x
)
g
(
x
)
d
x
=
f
(
x
)
g
(
−
1
)
(
x
)
−
∫
f
′
(
x
)
g
(
−
1
)
(
x
)
d
x
=
f
(
x
)
g
(
−
1
)
(
x
)
−
f
′
(
x
)
g
(
−
2
)
(
x
)
+
∫
f
″
(
x
)
g
(
−
2
)
(
x
)
d
x
=
f
(
x
)
g
(
−
1
)
(
x
)
−
f
′
(
x
)
g
(
−
2
)
(
x
)
+
f
″
(
x
)
g
(
−
3
)
(
x
)
+
⋯
+
(
−
1
)
n
∫
f
(
n
)
(
x
)
g
(
−
n
)
(
x
)
d
x
{\displaystyle {\begin{aligned}\int f(x)g(x)\,dx&=f(x)g^{(-1)}(x)-\int f'(x)g^{(-1)}(x)\,dx\\&=f(x)g^{(-1)}(x)-f'(x)g^{(-2)}(x)+\int f''(x)g^{(-2)}(x)\,dx\\&=f(x)g^{(-1)}(x)-f'(x)g^{(-2)}(x)+f''(x)g^{(-3)}(x)+\cdots +(-1)^{n}\int f^{(n)}(x)g^{(-n)}(x)\,dx\end{aligned}}}
となる。 ここで、
g
(
−
1
)
(
x
)
{\displaystyle g^{(-1)}(x)}
g
(
x
)
{\displaystyle g(x)}
g
(
−
2
)
(
x
)
{\displaystyle g^{(-2)}(x)}
g
(
−
1
)
(
x
)
{\displaystyle g^{(-1)}(x)}
g
(
−
n
)
(
x
)
{\displaystyle g^{(-n)}(x)}
g
(
−
n
+
1
)
(
x
)
{\displaystyle g^{(-n+1)}(x)}
符号
微分
積分
+
{\displaystyle +}
f
(
x
)
{\displaystyle f(x)}
g
(
x
)
{\displaystyle g(x)}
−
{\displaystyle -}
f
′
(
x
)
{\displaystyle f'(x)}
g
(
−
1
)
(
x
)
{\displaystyle g^{(-1)}(x)}
+
{\displaystyle +}
f
″
(
x
)
{\displaystyle f''(x)}
g
(
−
2
)
(
x
)
{\displaystyle g^{(-2)}(x)}
−
{\displaystyle -}
f
(
3
)
(
x
)
{\displaystyle f^{(3)}(x)}
g
(
−
3
)
(
x
)
{\displaystyle g^{(-3)}(x)}
⋯
{\displaystyle \cdots }
⋯
{\displaystyle \cdots }
⋯
{\displaystyle \cdots }
(
−
)
n
{\displaystyle (-)^{n}}
f
(
n
)
(
x
)
{\displaystyle f^{(n)}(x)}
g
(
−
n
)
(
x
)
{\displaystyle g^{(-n)}(x)}
この表から、部分積分を
n
{\displaystyle n}
一行目の符号 × 一行目の微分 × 二行目の積分 + 二行目の符号 × 二行目の微分 × 三行目の積分 + ... +
∫
{\displaystyle \int }
と求まる。n行目の微分 が 0 であった場合は、最後の積分は消えて、不定積分は
一行目の符号 × 一行目の微分 × 二行目の積分 + 二行目の符号 × 二行目の微分 × 三行目の積分 + ... + n-1行目の符号 × n-1行目の微分 × n行目の積分 + C
となる。
この方法は俗に瞬間部分積分法 と呼ばれており、部分積分を複数回繰り返す際の計算を非常に簡略化できるため、受験数学では重宝されるテクニックの一つである。記述で用いる場合、上の表をそのまま記述するよりも、「部分積分を繰り返し用いると」という文言の後に瞬間部分積分で求めた結果を記述するのが無難である。
n
≠
−
1
{\displaystyle n\neq -1}
(
1
n
+
1
x
n
+
1
)
′
=
x
n
{\displaystyle \left({\frac {1}{n+1}}x^{n+1}\right)'=x^{n}}
∫
x
n
d
x
=
1
n
+
1
x
n
+
1
+
C
{\displaystyle \int x^{n}dx={\frac {1}{n+1}}x^{n+1}+C}
n
=
−
1
{\displaystyle n=-1}
(
log
|
x
|
)
′
=
1
x
=
x
−
1
{\displaystyle (\log |x|)'={\frac {1}{x}}=x^{-1}}
∫
x
−
1
d
x
=
∫
1
x
d
x
=
log
|
x
|
+
C
{\displaystyle \int x^{-1}dx=\int {\frac {1}{x}}dx=\log |x|+C}
が成り立つ。
(
sin
x
)
′
=
cos
x
{\displaystyle (\sin x)'=\cos x}
(
cos
x
)
′
=
−
sin
x
{\displaystyle (\cos x)'=-\sin x}
(
tan
x
)
′
=
1
cos
2
x
{\displaystyle (\tan x)'={\frac {1}{\cos ^{2}x}}}
が成り立つことを考慮すると、
∫
cos
x
d
x
=
sin
x
+
C
{\displaystyle \int \cos xdx=\sin x+C}
∫
sin
x
d
x
=
−
cos
x
+
C
{\displaystyle \int \sin xdx=-\cos x+C}
∫
1
cos
2
x
d
x
=
tan
x
+
C
{\displaystyle \int {\frac {1}{\cos ^{2}x}}dx=\tan x+C}
となることが分る。
∫
tan
x
d
x
{\displaystyle \int \tan xdx}
∫
tan
x
d
x
{\displaystyle \int \tan xdx}
=
∫
sin
x
cos
x
d
x
{\displaystyle =\int {\frac {\sin x}{\cos x}}dx}
=
∫
−
(
cos
x
)
′
cos
x
d
x
{\displaystyle =\int {\frac {-(\cos x)'}{\cos x}}dx}
=
−
∫
(
cos
x
)
′
cos
x
d
x
{\displaystyle =-\int {\frac {(\cos x)'}{\cos x}}dx}
=
−
log
|
cos
x
|
+
C
{\displaystyle =-\log |\cos x|+C}
なお同様に、
1
tan
x
=
cos
x
sin
x
{\displaystyle {\frac {1}{\tan x}}={\frac {\cos x}{\sin x}}}
∫
1
tan
x
d
x
=
∫
cos
x
sin
x
d
x
=
∫
(
sin
x
)
′
sin
x
d
x
=
log
|
sin
x
|
+
C
{\displaystyle \int {\frac {1}{\tan x}}dx=\int {\frac {\cos x}{\sin x}}dx=\int {\frac {(\sin x)'}{\sin x}}dx=\log \left|\sin x\right|+C}
より一般に有理関数
R
(
x
,
y
)
{\displaystyle R(x,y)}
∫
R
(
sin
θ
,
cos
θ
)
d
θ
{\displaystyle \int R(\sin \theta ,\cos \theta )\,d\theta }
t
=
tan
θ
2
{\displaystyle t=\tan {\frac {\theta }{2}}}
tan
2
θ
2
+
1
=
1
cos
2
θ
2
{\displaystyle \tan ^{2}{\frac {\theta }{2}}+1={\frac {1}{\cos ^{2}{\frac {\theta }{2}}}}}
cos
2
θ
2
=
1
1
+
t
2
{\displaystyle \cos ^{2}{\frac {\theta }{2}}={\frac {1}{1+t^{2}}}}
d
t
d
θ
=
d
d
θ
tan
θ
2
=
1
2
cos
2
θ
2
=
1
2
(
t
2
+
1
)
{\displaystyle {\frac {dt}{d\theta }}={\frac {d}{d\theta }}\tan {\frac {\theta }{2}}={\frac {1}{2\cos ^{2}{\frac {\theta }{2}}}}={\frac {1}{2}}(t^{2}+1)}
cos
θ
=
2
cos
2
θ
2
−
1
=
1
−
t
2
1
+
t
2
{\displaystyle \cos \theta =2\cos ^{2}{\frac {\theta }{2}}-1={\frac {1-t^{2}}{1+t^{2}}}}
sin
θ
=
tan
θ
cos
θ
=
2
tan
θ
2
1
−
tan
2
θ
2
cos
θ
=
2
t
1
+
t
2
{\displaystyle \sin \theta =\tan \theta \cos \theta ={\frac {2\tan {\frac {\theta }{2}}}{1-\tan ^{2}{\frac {\theta }{2}}}}\cos \theta ={\frac {2t}{1+t^{2}}}}
である。よって
∫
R
(
sin
θ
,
cos
θ
)
d
θ
=
∫
R
(
2
t
1
+
t
2
,
1
−
t
2
1
+
t
2
)
2
d
t
1
+
t
2
{\displaystyle \int R(\sin \theta ,\cos \theta )\,d\theta =\int R\left({\frac {2t}{1+t^{2}}},{\frac {1-t^{2}}{1+t^{2}}}\right)\,{\frac {2dt}{1+t^{2}}}}
と有理関数の積分にもち込める。
幾何学的は、この変換は単位円上の点
P
(
cos
θ
,
sin
θ
)
{\displaystyle P(\cos \theta ,\sin \theta )}
A
(
−
1
,
0
)
{\displaystyle A(-1,0)}
t
{\displaystyle t}
∠
x
A
P
=
1
2
∠
x
O
P
=
θ
2
{\displaystyle \angle xAP={\frac {1}{2}}\angle xOP={\frac {\theta }{2}}}
t
=
tan
θ
2
.
{\displaystyle t=\tan {\frac {\theta }{2}}.}
被積分関数の周期が
π
{\displaystyle \pi }
sin
2
θ
,
cos
2
θ
{\displaystyle \sin 2\theta ,\cos 2\theta }
t
=
tan
θ
{\displaystyle t=\tan \theta }
sin
2
θ
,
cos
2
θ
,
sin
θ
cos
θ
{\displaystyle \sin ^{2}\theta ,\cos ^{2}\theta ,\sin \theta \cos \theta }
t
=
tan
θ
{\displaystyle t=\tan \theta }
cos
2
θ
=
1
1
+
tan
2
θ
=
1
1
+
t
2
{\displaystyle \cos ^{2}\theta ={\frac {1}{1+\tan ^{2}\theta }}={\frac {1}{1+t^{2}}}}
sin
2
θ
=
tan
2
θ
cos
2
θ
=
t
2
1
+
t
2
{\displaystyle \sin ^{2}\theta =\tan ^{2}\theta \cos ^{2}\theta ={\frac {t^{2}}{1+t^{2}}}}
sin
θ
cos
θ
=
±
sin
2
θ
cos
2
θ
=
t
1
+
t
2
{\displaystyle \sin \theta \cos \theta =\pm {\sqrt {\sin ^{2}\theta \cos ^{2}\theta }}={\frac {t}{1+t^{2}}}}
sin
θ
cos
θ
{\displaystyle \sin \theta \cos \theta }
tan
θ
=
sin
θ
cos
θ
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}}
d
θ
=
d
t
1
+
t
2
{\displaystyle d\theta ={\frac {dt}{1+t^{2}}}}
例
∫
1
sin
x
cos
x
d
x
{\displaystyle \int {\frac {1}{\sin x\cos x}}dx}
t
=
tan
x
{\displaystyle t=\tan x}
∫
1
sin
x
cos
x
d
x
=
∫
1
+
t
2
t
d
t
1
+
t
2
=
ln
|
tan
x
|
+
C
.
{\displaystyle \int {\frac {1}{\sin x\cos x}}dx=\int {\frac {1+t^{2}}{t}}{\frac {dt}{1+t^{2}}}=\ln |\tan x|+C.}
t
=
tan
θ
2
{\displaystyle t=\tan {\frac {\theta }{2}}}
∫
1
sin
x
cos
x
d
x
=
∫
1
+
t
2
t
(
1
−
t
2
)
d
t
=
ln
|
t
1
−
t
2
|
+
C
′
=
ln
|
tan
x
|
+
C
{\displaystyle \int {\frac {1}{\sin x\cos x}}\,dx=\int {\frac {1+t^{2}}{t(1-t^{2})}}\,dt=\ln \left|{\frac {t}{1-t^{2}}}\right|+C'=\ln |\tan x|+C}
指数関数について
(
e
x
)
′
=
e
x
{\displaystyle (e^{x})'=e^{x}}
∫
e
x
d
x
=
e
x
+
C
{\displaystyle \int e^{x}dx=e^{x}+C}
また、
(
a
x
ln
a
)
′
=
a
x
{\displaystyle \left({\frac {a^{x}}{\ln a}}\right)'=a^{x}}
∫
a
x
d
x
=
a
x
ln
a
{\displaystyle \int a^{x}\,dx={\frac {a^{x}}{\ln a}}}
また、
log
|
x
|
{\displaystyle \log |x|}
∫
log
|
x
|
d
x
{\displaystyle \int \log |x|dx}
=
∫
(
x
)
′
log
|
x
|
d
x
{\displaystyle =\int (x)'\log |x|dx}
=
x
log
|
x
|
−
∫
x
(
log
|
x
|
)
′
d
x
{\displaystyle =x\log |x|-\int x(\log |x|)'dx}
=
x
log
|
x
|
−
∫
x
1
x
d
x
{\displaystyle =x\log |x|-\int x{\frac {1}{x}}dx}
=
x
log
|
x
|
−
∫
d
x
{\displaystyle =x\log |x|-\int dx}
=
x
log
|
x
|
−
x
+
C
{\displaystyle =x\log |x|-x+C}
となる。
有理関数
R
(
x
)
{\displaystyle R(x)}
∫
R
(
e
x
)
d
x
{\displaystyle \int R(e^{x})\,dx}
t
=
e
x
{\displaystyle t=e^{x}}
d
t
d
x
=
e
x
=
t
{\displaystyle {\frac {dt}{dx}}=e^{x}=t}
∫
R
(
e
x
)
d
x
=
∫
R
(
t
)
d
t
t
.
{\displaystyle \int R(e^{x})\,dx=\int R(t){\frac {dt}{t}}.}
有理関数
R
(
x
,
y
)
{\displaystyle R(x,y)}
∫
R
(
x
,
a
x
2
+
b
x
+
c
)
d
x
{\displaystyle \int R(x,{\sqrt {ax^{2}+bx+c}})\,dx}
p
2
−
x
2
,
x
2
+
p
2
,
x
2
−
p
2
{\displaystyle {\sqrt {p^{2}-x^{2}}},{\sqrt {x^{2}+p^{2}}},{\sqrt {x^{2}-p^{2}}}}
x
=
p
sin
θ
,
x
=
p
tan
θ
,
x
=
p
cos
θ
{\displaystyle x=p\sin \theta ,x=p\tan \theta ,x={\frac {p}{\cos \theta }}}
また、
y
2
=
a
x
2
+
b
x
+
c
{\displaystyle y^{2}=ax^{2}+bx+c}
a
>
0
{\displaystyle a>0}
y
2
−
a
(
x
+
b
2
a
)
2
=
−
b
2
+
4
a
c
4
a
{\displaystyle y^{2}-a\left(x+{\frac {b}{2a}}\right)^{2}={\frac {-b^{2}+4ac}{4a}}}
[ 1]
y
=
±
a
x
+
t
{\displaystyle y=\pm {\sqrt {a}}x+t}
t
=
∓
a
x
+
a
x
2
+
b
x
+
c
{\displaystyle t=\mp {\sqrt {a}}x+{\sqrt {ax^{2}+bx+c}}}
t
{\displaystyle t}
y
=
±
a
x
+
t
{\displaystyle y=\pm {\sqrt {a}}x+t}
(
x
,
y
)
{\displaystyle (x,y)}
t
{\displaystyle t}
例
∫
d
x
x
2
−
1
{\displaystyle \int {\frac {dx}{\sqrt {x^{2}-1}}}}
t
=
x
+
x
2
−
1
{\displaystyle t=x+{\sqrt {x^{2}-1}}}
1
t
=
x
−
x
2
−
1
{\displaystyle {\frac {1}{t}}=x-{\sqrt {x^{2}-1}}}
t
+
1
t
=
2
x
{\displaystyle t+{\frac {1}{t}}=2x}
2
d
x
=
(
1
−
1
t
2
)
d
t
{\displaystyle 2dx=\left(1-{\frac {1}{t^{2}}}\right)dt}
t
−
1
t
=
2
x
2
−
1
{\displaystyle t-{\frac {1}{t}}=2{\sqrt {x^{2}-1}}}
∫
d
x
x
2
−
1
=
∫
1
−
1
t
2
t
−
1
t
d
t
=
∫
d
t
t
=
ln
|
x
+
x
2
−
1
|
+
C
{\displaystyle \int {\frac {dx}{\sqrt {x^{2}-1}}}=\int {\frac {1-{\frac {1}{t^{2}}}}{t-{\frac {1}{t}}}}dt=\int {\frac {dt}{t}}=\ln |x+{\sqrt {x^{2}-1}}|+C}
ところで、この変換は双曲線
y
2
=
x
2
−
1
{\displaystyle y^{2}=x^{2}-1}
y
=
−
x
+
t
{\displaystyle y=-x+t}
t
{\displaystyle t}
x
=
1
2
(
t
+
1
t
)
,
y
=
1
2
(
t
−
1
t
)
{\displaystyle x={\frac {1}{2}}\left(t+{\frac {1}{t}}\right),\,y={\frac {1}{2}}\left(t-{\frac {1}{t}}\right)}
t
→
e
t
{\displaystyle t\rightarrow e^{t}}
x
=
e
t
+
e
−
t
2
=
cosh
t
,
y
=
e
t
−
e
−
t
2
=
sinh
t
.
{\displaystyle x={\frac {e^{t}+e^{-t}}{2}}=\cosh t,\,y={\frac {e^{t}-e^{-t}}{2}}=\sinh t.}
x
>
0
{\displaystyle x>0}
h
{\displaystyle \mathrm {h} }
cosh
2
t
−
sinh
2
t
=
1
{\displaystyle \cosh ^{2}t-\sinh ^{2}t=1}
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
x
=
cosh
t
{\displaystyle x=\cosh t}
定積分について、不定積分と同じように以下が成り立つ。
定積分の置換積分法
α
<
β
{\displaystyle \alpha <\beta }
[
α
,
β
]
{\displaystyle [\alpha ,\beta ]}
x
=
g
(
t
)
{\displaystyle x=g(t)}
a
=
g
(
α
)
,
b
=
g
(
β
)
{\displaystyle a=g(\alpha ),b=g(\beta )}
∫
a
b
f
(
x
)
d
x
=
∫
α
β
f
(
g
(
t
)
)
g
′
(
t
)
d
t
{\displaystyle \int _{a}^{b}f(x)\,dx=\int _{\alpha }^{\beta }f(g(t))g'(t)\,dt}
定積分の部分積分法
∫
a
b
f
(
x
)
g
′
(
x
)
d
x
=
[
f
(
x
)
g
(
x
)
]
b
a
−
∫
a
b
f
′
(
x
)
g
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)g'(x)\,dx=\left[f(x)g(x)\right]_{b}^{a}-\int _{a}^{b}f'(x)g(x)\,dx}
問題
以下の定積分を求めよ(Hint:5, 6は漸化式を利用する)
∫
0
1
|
e
x
−
3
2
|
d
x
{\displaystyle \int _{0}^{1}|e^{x}-{\frac {3}{2}}|\,dx}
∫
1
0
x
−
2
(
3
−
x
)
2
d
x
{\displaystyle \int _{1}^{0}{\frac {x-2}{(3-x)^{2}}}\,dx}
∫
−
5
5
x
x
2
−
9
d
x
{\displaystyle \int _{-5}^{5}x{\sqrt {x^{2}-9}}\,dx}
∫
3
7
x
log
(
x
2
−
2
)
d
x
{\displaystyle \int _{3}^{7}x\log(x^{2}-2)\,dx}
∫
0
π
2
sin
n
x
d
x
{\displaystyle \int _{0}^{\frac {\pi }{2}}\sin ^{n}x\,dx}
∫
0
π
4
tan
n
x
d
x
{\displaystyle \int _{0}^{\frac {\pi }{4}}\tan ^{n}x\,dx}
a
<
b
{\displaystyle a<b}
∫
a
b
(
x
−
a
)
(
b
−
x
)
d
x
{\displaystyle \int _{a}^{b}{\sqrt {(x-a)(b-x)}}\,dx}
y
=
(
x
−
a
)
(
b
−
x
)
{\displaystyle y={\sqrt {(x-a)(b-x)}}}
(
x
−
a
+
b
2
)
+
y
2
=
(
a
−
b
2
)
2
{\displaystyle \left(x-{\frac {a+b}{2}}\right)+y^{2}=\left({\frac {a-b}{2}}\right)^{2}}
y
{\displaystyle y}
a
+
b
2
{\displaystyle {\frac {a+b}{2}}}
b
−
a
2
{\displaystyle {\frac {b-a}{2}}}
∫
a
b
(
x
−
a
)
(
b
−
x
)
d
x
=
π
2
(
b
−
a
2
)
2
{\displaystyle \int _{a}^{b}{\sqrt {(x-a)(b-x)}}\,dx={\frac {\pi }{2}}\left({\frac {b-a}{2}}\right)^{2}}
一般に、関数
f
(
a
−
x
)
{\displaystyle f(a-x)}
f
(
x
)
{\displaystyle f(x)}
x
=
a
2
{\displaystyle x={\frac {a}{2}}}
従って、連続関数
f
(
x
)
{\displaystyle f(x)}
[
a
+
b
2
,
b
]
{\displaystyle \left[{\frac {a+b}{2}},b\right]}
∫
a
+
b
2
b
f
(
x
)
d
x
{\displaystyle \int _{\frac {a+b}{2}}^{b}f(x)\,dx}
f
(
a
+
b
−
x
)
{\displaystyle f(a+b-x)}
[
a
,
a
+
b
2
]
{\displaystyle \left[a,{\frac {a+b}{2}}\right]}
∫
a
a
+
b
2
f
(
a
+
b
−
x
)
d
x
{\displaystyle \int _{a}^{\frac {a+b}{2}}f(a+b-x)\,dx}
∫
a
+
b
2
b
f
(
x
)
d
x
=
∫
a
a
+
b
2
f
(
a
+
b
−
x
)
d
x
.
{\displaystyle \int _{\frac {a+b}{2}}^{b}f(x)\,dx=\int _{a}^{\frac {a+b}{2}}f(a+b-x)\,dx.}
この等式は単に、
x
→
a
+
b
−
x
{\displaystyle x\to a+b-x}
この等式より、
∫
a
b
f
(
x
)
d
x
=
∫
a
a
+
b
2
f
(
x
)
d
x
+
∫
a
+
b
2
b
f
(
x
)
d
x
=
∫
a
a
+
b
2
[
f
(
x
)
+
f
(
a
+
b
−
x
)
]
d
x
{\displaystyle \int _{a}^{b}f(x)\,dx=\int _{a}^{\frac {a+b}{2}}f(x)\,dx+\int _{\frac {a+b}{2}}^{b}f(x)\,dx=\int _{a}^{\frac {a+b}{2}}[f(x)+f(a+b-x)]\,dx}
この公式は、
f
(
x
)
+
f
(
a
+
b
−
x
)
{\displaystyle f(x)+f(a+b-x)}
例えば、
∫
0
π
2
sin
x
sin
x
+
cos
x
d
x
=
∫
0
π
4
[
sin
x
sin
x
+
cos
x
+
sin
(
π
2
−
x
)
sin
(
π
2
−
x
)
+
cos
(
π
2
−
x
)
]
d
x
=
∫
0
π
4
[
sin
x
sin
x
+
cos
x
+
cos
x
cos
x
+
sin
x
]
d
x
=
∫
0
π
4
d
x
=
π
4
.
{\displaystyle {\begin{aligned}\int _{0}^{\frac {\pi }{2}}{\frac {\sin x}{\sin x+\cos x}}\,dx&=\int _{0}^{\frac {\pi }{4}}\left[{\frac {\sin x}{\sin x+\cos x}}+{\frac {\sin({\frac {\pi }{2}}-x)}{\sin({\frac {\pi }{2}}-x)+\cos({\frac {\pi }{2}}-x)}}\right]\,dx\\&=\int _{0}^{\frac {\pi }{4}}\left[{\frac {\sin x}{\sin x+\cos x}}+{\frac {\cos x}{\cos x+\sin x}}\right]\,dx\\&=\int _{0}^{\frac {\pi }{4}}dx={\frac {\pi }{4}}.\end{aligned}}}
∫
−
1
1
x
2
1
+
e
x
d
x
=
1
3
{\displaystyle \int _{-1}^{1}{\frac {x^{2}}{1+e^{x}}}\,dx={\frac {1}{3}}}
∫
0
π
4
ln
(
1
+
tan
x
)
d
x
=
π
8
log
2
{\displaystyle \int _{0}^{\frac {\pi }{4}}\ln(1+\tan x)\,dx={\frac {\pi }{8}}\log 2}
∫
0
π
2
ln
sin
x
d
x
=
−
π
2
log
2
{\displaystyle \int _{0}^{\frac {\pi }{2}}\ln \sin x\,dx=-{\frac {\pi }{2}}\log 2}
一般に、連続関数について次のことが成り立つ。
開区間
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
≦
g
(
x
)
{\displaystyle f(x)\leqq g(x)}
∫
a
b
f
(
x
)
d
x
≦
∫
a
b
g
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,dx\leqq \int _{a}^{b}g(x)\,dx}
等号成立条件は開区間
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
=
g
(
x
)
{\displaystyle f(x)=g(x)}
調和級数の第n部分和が
log
(
n
+
1
)
{\displaystyle \log(n+1)}
自然数kに対して
k
≦
x
≦
k
+
1
{\displaystyle k\leqq x\leqq k+1}
1
k
≧
1
x
{\displaystyle {\frac {1}{k}}\geqq {\frac {1}{x}}}
∫
k
k
+
1
d
x
k
>
∫
k
k
+
1
d
x
x
{\displaystyle \int _{k}^{k+1}{\frac {dx}{k}}>\int _{k}^{k+1}{\frac {dx}{x}}}
∑
k
=
1
n
∫
k
k
+
1
d
x
k
>
∑
k
=
1
n
∫
k
k
+
1
d
x
x
{\displaystyle \sum _{k=1}^{n}\int _{k}^{k+1}{\frac {dx}{k}}>\sum _{k=1}^{n}\int _{k}^{k+1}{\frac {dx}{x}}}
このとき、(左辺)
=
∑
k
=
1
n
1
k
∫
k
k
+
1
d
x
=
∑
k
=
1
n
1
k
{\displaystyle =\sum _{k=1}^{n}{\frac {1}{k}}\int _{k}^{k+1}dx=\sum _{k=1}^{n}{\frac {1}{k}}}
=
∑
k
=
1
n
∫
k
k
+
1
d
x
x
=
∫
1
n
+
1
d
x
x
=
[
log
(
x
)
]
1
n
+
1
=
log
(
n
+
1
)
−
log
(
1
)
=
log
(
n
+
1
)
{\displaystyle =\sum _{k=1}^{n}\int _{k}^{k+1}{\frac {dx}{x}}=\int _{1}^{n+1}{\frac {dx}{x}}=\left[\log(x)\right]_{1}^{n+1}=\log(n+1)-\log(1)=\log(n+1)}
演習問題1
次の不定積分を求めよ。
(1)
∫
tan
x
d
x
{\displaystyle \int \tan xdx}
(2)
∫
1
cos
2
x
d
x
{\displaystyle \int {\frac {1}{\cos ^{2}x}}dx}
(3)
∫
log
x
d
x
{\displaystyle \int \log xdx}
(4)
∫
x
log
x
d
x
{\displaystyle \int x\log xdx}
(5)
∫
x
2
log
x
d
x
{\displaystyle \int x^{2}\log xdx}
(6)
∫
x
3
log
x
d
x
{\displaystyle \int x^{3}\log xdx}
(7)
∫
x
sin
x
d
x
{\displaystyle \int x\sin xdx}
(8)
∫
x
2
sin
x
d
x
{\displaystyle \int x^{2}\sin xdx}
(9)
∫
x
2
e
x
d
x
{\displaystyle \int x^{2}e^{x}dx}
(1)
−
log
(
cos
x
)
+
C
{\displaystyle -\log(\cos x)+C}
(2)
tan
x
+
C
{\displaystyle \tan x+C}
(3)
x
log
x
−
x
+
C
{\displaystyle x\log x-x+C}
(4)
x
2
log
x
2
−
x
2
4
+
C
{\displaystyle {\frac {x^{2}\log x}{2}}-{\frac {x^{2}}{4}}+C}
(5)
x
3
log
x
3
−
x
3
9
+
C
{\displaystyle {\frac {x^{3}\log x}{3}}-{\frac {x^{3}}{9}}+C}
(6)
x
4
log
x
4
−
x
4
16
+
C
{\displaystyle {\frac {x^{4}\log x}{4}}-{\frac {x^{4}}{16}}+C}
(7)
sin
x
−
x
cos
x
+
C
{\displaystyle \sin x-x\cos x+C}
(8)
2
x
sin
x
+
(
2
−
x
2
)
cos
x
+
C
{\displaystyle 2x\sin x+(2-x^{2})\cos x+C}
(9)
(
x
2
−
2
x
+
2
)
e
x
+
C
{\displaystyle (x^{2}-2x+2)e^{x}+C}
演習問題2
第一問(Wallis の積分)
n
{\displaystyle n}
I
n
=
∫
0
π
2
sin
n
x
d
x
{\displaystyle I_{n}=\int _{0}^{\frac {\pi }{2}}\sin ^{n}x\,dx}
(1)
∫
0
π
2
sin
n
x
d
x
=
∫
0
π
2
cos
n
x
d
x
{\displaystyle \int _{0}^{\frac {\pi }{2}}\sin ^{n}x\,dx=\int _{0}^{\frac {\pi }{2}}\cos ^{n}x\,dx}
(2)
I
n
=
n
−
1
n
I
n
−
2
(
n
≥
2
)
{\displaystyle I_{n}={\frac {n-1}{n}}I_{n-2}\quad (n\geq 2)}
(3)
I
n
{\displaystyle I_{n}}
第二問(ベータ関数の特殊値)
m
,
n
{\displaystyle m,n}
α
,
β
{\displaystyle \alpha ,\beta }
β
>
α
{\displaystyle \beta >\alpha }
I
m
,
n
=
∫
α
β
(
x
−
α
)
m
(
β
−
x
)
n
d
x
{\displaystyle I_{m,n}=\int _{\alpha }^{\beta }(x-\alpha )^{m}(\beta -x)^{n}\,dx}
(1)
I
m
,
n
=
n
m
+
1
I
m
+
1
,
n
−
1
(
n
≥
1
)
{\displaystyle I_{m,n}={\frac {n}{m+1}}I_{m+1,n-1}\quad (n\geq 1)}
(2)
I
m
,
n
{\displaystyle I_{m,n}}
(3)
∫
0
π
2
sin
2
m
+
1
θ
cos
2
n
+
1
θ
d
θ
{\displaystyle \int _{0}^{\frac {\pi }{2}}\sin ^{2m+1}\theta \cos ^{2n+1}\theta d\theta }
ある関数f(x)の原始関数を求める演算は
f(x)とx軸にはさまれた領域の面積を求める演算に等しい。
このことを用いて
ある関数によって作られた領域の面積を求めることが出来る。
x^2の0から1までの積分 例えば、
∫
0
1
x
2
d
x
=
1
3
{\displaystyle \int _{0}^{1}x^{2}dx={\frac {1}{3}}}
y
=
x
2
{\displaystyle y=x^{2}}
0
<
x
<
1
{\displaystyle 0<x<1}
面積(Ⅰ)
曲線
y
=
f
(
x
)
{\displaystyle y=f(x)}
x
=
a
,
x
=
b
{\displaystyle x=a,x=b}
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
≧
0
{\displaystyle f(x)\geqq 0}
S
=
∫
a
b
f
(
x
)
d
x
{\displaystyle S=\int _{a}^{b}f(x)dx}
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
≦
0
{\displaystyle f(x)\leqq 0}
S
=
−
∫
a
b
f
(
x
)
d
x
{\displaystyle S=-\int _{a}^{b}f(x)dx}
厳密な証明は既に数学Ⅱで扱った。
面積(Ⅱ)
2曲線
y
=
f
(
x
)
,
y
=
g
(
x
)
{\displaystyle y=f(x),y=g(x)}
x
=
a
,
x
=
b
{\displaystyle x=a,x=b}
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
≧
g
(
x
)
{\displaystyle f(x)\geqq g(x)}
S
=
∫
a
b
{
f
(
x
)
−
g
(
x
)
}
d
x
{\displaystyle S=\int _{a}^{b}\{f(x)-g(x)\}dx}
面積(Ⅲ)
2曲線
x
=
h
(
y
)
,
x
=
i
(
y
)
{\displaystyle x=h(y),x=i(y)}
y
=
c
,
y
=
d
{\displaystyle y=c,y=d}
[
c
,
d
]
{\displaystyle [c,d]}
h
(
y
)
≧
i
(
y
)
{\displaystyle h(y)\geqq i(y)}
S
=
∫
c
d
{
h
(
y
)
−
i
(
y
)
}
d
y
{\displaystyle S=\int _{c}^{d}\{h(y)-i(y)\}dy}
ガウス=グリーンの定理
ガウス=グリーンの定理 という以下のような公式が存在する。
閉曲面Sで囲まれた空間の領域をV、曲面の外向き法線の方向余弦を(l, m, n)、微分可能な関数をf, g, hとするとき、
∫
V
(
∂
f
∂
x
+
∂
g
∂
y
+
∂
h
∂
z
)
d
V
=
∫
S
(
f
l
+
g
m
+
h
n
)
d
S
{\displaystyle \int _{V}({\frac {\partial f}{\partial x}}+{\frac {\partial g}{\partial y}}+{\frac {\partial h}{\partial z}})dV=\int _{S}(fl+gm+hn)dS}
この定理を高校レベルの求積で使えるように調整すると、以下のようになる。
曲線
{
x
=
f
(
t
)
y
=
g
(
t
)
{\displaystyle {\begin{cases}x=f(t)\\y=g(t)\end{cases}}}
[
a
,
b
]
{\displaystyle [a,b]}
P
(
f
(
t
)
,
g
(
t
)
)
{\displaystyle P(f(t),g(t))}
O
P
{\displaystyle OP}
∫
a
b
1
2
{
x
g
′
(
t
)
−
y
f
′
(
t
)
}
d
t
{\displaystyle \int _{a}^{b}{\frac {1}{2}}\{xg'(t)-yf'(t)\}dt}
この定理を用いると、通常の積分で面積を求めるよりも遙かに計算量が少なくて済む。
もちろん記述では使えないが、答えのみ書けば良い場合や検算用のツールとしては非常に役立つ。
発展:極座標系における面積 極座標系 においても、直交座標系と同様に微積分を考えることができる。ここでは、その一例として極方程式で表された曲線における面積について扱う。
面積(Ⅳ)
曲線
r
=
r
(
θ
)
{\displaystyle r=r(\theta )}
θ
=
α
,
θ
=
β
{\displaystyle \theta =\alpha ,\theta =\beta }
S
=
∫
α
β
1
2
{
r
(
θ
)
}
2
d
θ
{\displaystyle S=\int _{\alpha }^{\beta }{\frac {1}{2}}\{r(\theta )\}^{2}d\theta }
基本的には直交座標の場合と同様である。
曲線
r
=
r
(
θ
)
{\displaystyle r=r(\theta )}
θ
=
α
,
θ
=
τ
{\displaystyle \theta =\alpha ,\theta =\tau }
S
(
τ
)
{\displaystyle S(\tau )}
Δ
τ
>
0
{\displaystyle \Delta \tau >0}
τ
+
Δ
τ
{\displaystyle \tau +\Delta \tau }
閉区間
[
τ
,
τ
+
Δ
τ
]
{\displaystyle [\tau ,\tau +\Delta \tau ]}
r
(
θ
)
{\displaystyle r(\theta )}
m
{\displaystyle m}
M
{\displaystyle M}
1
2
m
2
Δ
τ
≦
S
(
τ
+
Δ
τ
)
−
S
(
τ
)
≦
1
2
M
2
Δ
τ
{\displaystyle {\frac {1}{2}}m^{2}\Delta \tau \leqq S(\tau +\Delta \tau )-S(\tau )\leqq {\frac {1}{2}}M^{2}\Delta \tau }
上の不等式の各辺を
Δ
τ
{\displaystyle \Delta \tau }
1
2
m
2
≦
S
(
τ
+
Δ
τ
)
−
S
(
τ
)
Δ
τ
≦
1
2
M
2
{\displaystyle {\frac {1}{2}}m^{2}\leqq {\frac {S(\tau +\Delta \tau )-S(\tau )}{\Delta \tau }}\leqq {\frac {1}{2}}M^{2}}
Δ
τ
→
0
{\displaystyle \Delta \tau \to 0}
r
(
τ
)
{\displaystyle r(\tau )}
1
2
m
2
→
1
2
{
r
(
τ
)
}
2
,
1
2
M
2
→
1
2
{
r
(
τ
)
}
2
{\displaystyle {\frac {1}{2}}m^{2}\to {\frac {1}{2}}\{r(\tau )\}^{2},{\frac {1}{2}}M^{2}\to {\frac {1}{2}}\{r(\tau )\}^{2}}
微分の定義より
S
(
τ
+
Δ
τ
)
−
S
(
τ
)
Δ
τ
→
S
′
(
τ
)
{\displaystyle {\frac {S(\tau +\Delta \tau )-S(\tau )}{\Delta \tau }}\to S'(\tau )}
よってはさみうちの原理より
S
′
(
τ
)
=
1
2
{
r
(
τ
)
}
2
{\displaystyle S'(\tau )={\frac {1}{2}}\{r(\tau )\}^{2}}
これにて示された。 この公式は、
θ
{\displaystyle \theta }
θ
{\displaystyle \theta }
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
楕円の面積 楕円の面積
楕円
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}
S
=
π
a
b
{\displaystyle S=\pi ab}
楕円
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}
y
{\displaystyle y}
y
=
±
b
a
a
2
−
x
2
{\displaystyle y=\pm {\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}}
となる。そのうち
y
=
b
a
a
2
−
x
2
{\displaystyle y={\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}}
S となるので
S
=
2
∫
−
a
a
b
a
a
2
−
x
2
=
2
b
a
∫
−
a
a
a
2
−
x
2
=
2
b
a
×
π
a
2
2
=
π
a
b
{\displaystyle S=2\int _{-a}^{a}{\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}={\frac {2b}{a}}\int _{-a}^{a}{\sqrt {a^{2}-x^{2}}}={\frac {2b}{a}}\times {\frac {\pi a^{2}}{2}}=\pi ab}
となる。
ある立体
V
0
{\displaystyle V_{0}}
x
=
t
{\displaystyle x=t}
t
{\displaystyle t}
S
(
t
)
{\displaystyle S(t)}
x
=
a
{\displaystyle x=a}
x
=
b
{\displaystyle x=b}
a
<
b
{\displaystyle a<b}
S
(
t
)
{\displaystyle S(t)}
d
t
{\displaystyle dt}
[ 2]
S
(
t
)
d
t
{\displaystyle S(t)\,dt}
[
a
,
b
]
{\displaystyle [a,b]}
V
=
∫
a
b
S
(
t
)
d
t
{\displaystyle V=\int _{a}^{b}S(t)\,dt}
(例1)
O
(
0
,
0
,
0
)
,
A
(
1
,
0
,
0
)
,
B
(
1
,
1
,
0
)
,
C
(
1
,
0
,
2
)
{\displaystyle O(0,0,0),A(1,0,0),B(1,1,0),C(1,0,2)}
この三角錐を平面
x
=
t
(
0
≦
t
≦
1
)
{\displaystyle x=t(0\leqq t\leqq 1)}
A
t
(
t
,
0
,
0
)
,
B
t
(
t
,
t
,
0
)
,
C
t
(
t
,
0
,
2
t
)
{\displaystyle A_{t}(t,0,0),B_{t}(t,t,0),C_{t}(t,0,2t)}
△
A
t
B
t
C
t
{\displaystyle \triangle {A_{t}B_{t}C_{t}}}
S
(
t
)
=
t
2
{\displaystyle S(t)=t^{2}}
これを、区間
[
0
,
1
]
{\displaystyle [0,1]}
V
=
∫
0
1
S
(
t
)
d
t
=
∫
0
1
t
2
d
t
=
[
t
3
3
]
0
1
=
1
3
{\displaystyle V=\int _{0}^{1}S(t)\,dt=\int _{0}^{1}t^{2}\,dt=\left[{\frac {t^{3}}{3}}\right]_{0}^{1}={\frac {1}{3}}}
[ 3] (例2)
設問
O
(
0
,
0
,
0
)
,
A
(
1
,
0
,
0
)
,
B
(
0
,
1
,
0
)
,
C
(
1
,
1
,
0
)
,
D
(
0
,
0
,
1
)
,
E
(
1
,
0
,
1
)
,
F
(
0
,
1
,
1
)
,
G
(
1
,
1
,
1
)
{\displaystyle O(0,0,0),A(1,0,0),B(0,1,0),C(1,1,0),D(0,0,1),E(1,0,1),F(0,1,1),G(1,1,1)}
平面
x
=
t
(
0
≦
t
≦
1
)
{\displaystyle x=t(0\leqq t\leqq 1)}
◻
O
t
A
t
B
t
C
t
{\displaystyle \square {O_{t}A_{t}B_{t}C_{t}}}
線分
O
t
A
t
,
A
t
B
t
,
B
t
C
t
,
C
t
O
t
{\displaystyle O_{t}A_{t},A_{t}B_{t},B_{t}C_{t},C_{t}O_{t}}
O
t
,
A
t
,
B
t
,
C
t
{\displaystyle O_{t},A_{t},B_{t},C_{t}}
t
{\displaystyle t}
H
t
,
I
t
,
J
t
,
K
t
{\displaystyle H_{t},I_{t},J_{t},K_{t}}
◻
H
t
I
t
J
t
K
t
{\displaystyle \square {H_{t}I_{t}J_{t}K_{t}}}
S
t
{\displaystyle S_{t}}
t
{\displaystyle t}
[
0
,
1
]
{\displaystyle [0,1]}
S
t
{\displaystyle S_{t}}
V
{\displaystyle V}
S
t
{\displaystyle S_{t}}
解答
S
t
{\displaystyle S_{t}}
l
{\displaystyle l}
l
2
=
t
2
+
(
1
−
t
)
2
=
2
t
2
−
2
t
+
1
{\displaystyle l^{2}=t^{2}+(1-t)^{2}=2t^{2}-2t+1}
S
t
{\displaystyle S_{t}}
S
(
t
)
{\displaystyle S(t)}
l
2
{\displaystyle l^{2}}
S
(
t
)
=
2
t
2
−
2
t
+
1
{\displaystyle S(t)=2t^{2}-2t+1}
これを、区間
[
0
,
1
]
{\displaystyle [0,1]}
V
=
∫
0
1
S
(
t
)
d
t
=
∫
0
1
(
2
t
2
−
2
t
+
1
)
d
t
=
[
2
t
3
3
−
t
2
+
t
]
0
1
=
2
3
{\displaystyle V=\int _{0}^{1}S(t)\,dt=\int _{0}^{1}(2t^{2}-2t+1)\,dt=\left[{\frac {2t^{3}}{3}}-t^{2}+t\right]_{0}^{1}={\frac {2}{3}}}
y
=
f
(
x
)
(
a
≤
x
≤
b
)
{\displaystyle y=f(x)(a\leq x\leq b)}
V
=
∫
a
b
π
{
f
(
x
)
}
2
d
x
{\displaystyle V=\int _{a}^{b}\pi \{f(x)\}^{2}dx}
立体をx軸に垂直であり、x=cを満たす面とx=c+hを満たす面で切ると(hは小さな
定数)、その切断面で挟まれた立体は半径 f(c)の円と半径 f(c+h)の円
ではさまれた立体となる。
しかし、hが極めて小さいとき、この図形は半径f(c),高さhの円柱で
近似できる。
よってこの2つの面に関して、得られた図形の体積は
h
×
π
(
f
(
c
)
)
2
{\displaystyle h\times \pi (f(c))^{2}}
a
<
c
<
b
{\displaystyle a<c<b}
S
=
∫
a
b
π
(
f
(
x
)
)
2
d
x
{\displaystyle S=\int _{a}^{b}\pi (f(x))^{2}dx}
x
=
g
(
y
)
(
c
≤
x
≤
d
)
{\displaystyle x=g(y)(c\leq x\leq d)}
V
=
∫
c
d
π
{
g
(
y
)
}
2
d
y
{\displaystyle V=\int _{c}^{d}\pi \{g(y)\}^{2}dy}
で与えられる。
例えば、
y
=
x
2
(
0
<
x
<
1
)
{\displaystyle y=x^{2}~(0<x<1)}
図形の絵?
S
=
∫
0
1
π
(
x
2
)
2
d
x
{\displaystyle S=\int _{0}^{1}\pi (x^{2})^{2}dx}
=
π
∫
0
1
x
4
d
x
{\displaystyle =\pi \int _{0}^{1}x^{4}dx}
=
π
5
{\displaystyle ={\frac {\pi }{5}}}
球の体積 球の体積
V
=
4
3
π
r
3
{\displaystyle V={\frac {4}{3}}\pi r^{3}}
半径r の球は半円
y
=
r
2
−
x
2
{\displaystyle y={\sqrt {r^{2}-x^{2}}}}
x 軸の周りに回転させてつくることができる。
V
=
π
∫
−
r
r
r
2
−
x
2
2
d
x
=
π
∫
−
r
r
(
r
2
−
x
2
)
d
x
=
4
3
π
r
3
{\displaystyle V=\pi \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}^{2}dx=\pi \int _{-r}^{r}(r^{2}-x^{2})dx={\frac {4}{3}}\pi r^{3}}
また体積をr で微分すると球の表面積
S
=
4
π
r
2
{\displaystyle S=4\pi r^{2}}
補:バームクーヘン積分 上記の回転体の公式の導出では「円盤の面積を積分」しているが、「円筒の側面積」を積分しても同様の結果が得られる。この考え方をバームクーヘン積分(円筒分割積分) と呼ぶ。
バームクーヘン積分による回転体の体積の公式
曲線
y
=
f
(
x
)
{\displaystyle y=f(x)}
x
=
a
,
x
=
b
{\displaystyle x=a,x=b}
V
=
2
π
∫
a
b
x
f
(
x
)
d
x
{\displaystyle V=2\pi \int _{a}^{b}xf(x)dx}
閉区間
[
x
,
x
+
Δ
x
]
(
Δ
x
>
0
)
{\displaystyle [x,x+\Delta x](\Delta x>0)}
y
=
f
(
x
)
{\displaystyle y=f(x)}
Δ
V
{\displaystyle \Delta V}
このとき、
π
{
(
x
+
Δ
x
)
2
−
x
2
}
m
≦
Δ
V
≦
π
{
(
x
+
Δ
x
)
2
−
x
2
}
M
{\displaystyle \pi \{(x+\Delta x)^{2}-x^{2}\}m\leqq \Delta V\leqq \pi \{(x+\Delta x)^{2}-x^{2}\}M}
変形すると
π
(
2
x
+
Δ
x
)
m
≦
Δ
V
Δ
x
≦
π
(
2
x
+
Δ
x
)
M
{\displaystyle \pi (2x+\Delta x)m\leqq {\frac {\Delta V}{\Delta x}}\leqq \pi (2x+\Delta x)M}
lim
Δ
x
→
+
0
m
=
lim
Δ
x
→
+
0
M
=
f
(
x
)
{\displaystyle \lim _{\Delta x\to +0}m=\lim _{\Delta x\to +0}M=f(x)}
lim
Δ
x
→
+
0
Δ
V
Δ
x
=
2
π
x
f
(
x
)
{\displaystyle \lim _{\Delta x\to +0}{\frac {\Delta V}{\Delta x}}=2\pi xf(x)}
∴
d
V
d
x
=
2
π
x
f
(
x
)
{\displaystyle \therefore {\frac {dV}{dx}}=2\pi xf(x)}
Δ
x
<
0
{\displaystyle \Delta x<0}
この微分方程式を解く(詳細はこちら )と、
d
V
=
2
π
x
f
(
x
)
d
x
{\displaystyle dV=2\pi xf(x)dx}
∫
d
V
=
∫
2
π
x
f
(
x
)
d
x
{\displaystyle \int dV=\int 2\pi xf(x)dx}
V
=
2
π
∫
x
f
(
x
)
d
x
+
C
{\displaystyle V=2\pi \int xf(x)dx+C}
閉区間
[
a
,
b
]
{\displaystyle [a,b]}
V
=
2
π
∫
a
b
x
f
(
x
)
d
x
{\displaystyle V=2\pi \int _{a}^{b}xf(x)dx}
記述問題で用いる場合、念のため上のように証明しておくと良い。
補:パップス・ギュルダンの定理 図形Aを、図形Aと交わらない直線の周りに一回転してできる立体の体積は、V=(Aの重心が描く円の円周長)×(Aの面積)で求まる。
この定理は大学入試においては非常に有名な裏技であり知っておいて損はないが、記述で用いると完全にアウトである。この定理を用いるのは、選択肢形式の問題かどうしても記述の白紙解答を避けたい場合のみに限ろう。(もっとも、重心がわかる図形で出題されるのはごく稀だが。)
一般の軸を中心とした回転体の体積の求め方
一般に空間中の直線Lの周りの回転体(斜軸回転体 )の体積は、回転軸Lに垂直な平面で回転体を切った断面積を考えて求めることができる。
ここでは、回転前の図形が座標平面上に存在する場合を扱う。
例題 xy平面において
L
:
y
=
x
,
C
:
y
=
x
2
{\displaystyle L:y=x,C:y=x^{2}}
解答)
曲線C上の点
P
(
x
,
x
2
)
{\displaystyle P(x,x^{2})}
H
(
t
,
t
)
{\displaystyle H(t,t)}
Q
(
x
,
x
)
{\displaystyle Q(x,x)}
与えられた条件より
0
≦
x
≦
1
{\displaystyle 0\leqq x\leqq 1}
このとき
P
H
¯
=
|
x
−
x
2
|
2
=
x
−
x
2
2
(
∵
0
≦
x
≦
1
⟹
x
≧
x
2
)
{\displaystyle {\overline {PH}}={\frac {|x-x^{2}|}{\sqrt {2}}}={\frac {x-x^{2}}{\sqrt {2}}}(\because 0\leqq x\leqq 1\implies x\geqq x^{2})}
t
=
O
H
¯
=
O
Q
¯
−
H
Q
¯
=
O
Q
¯
−
P
H
¯
=
2
x
−
x
−
x
2
2
=
x
+
x
2
2
{\displaystyle t={\overline {OH}}={\overline {OQ}}-{\overline {HQ}}={\overline {OQ}}-{\overline {PH}}={\sqrt {2}}x-{\frac {x-x^{2}}{\sqrt {2}}}={\frac {x+x^{2}}{\sqrt {2}}}}
∴
d
t
=
1
+
2
x
2
d
x
{\displaystyle \therefore dt={\frac {1+2x}{\sqrt {2}}}dx}
tの積分範囲は0→√2なので、xの積分範囲は0→1である。
故に、
V
=
π
∫
0
2
P
H
¯
2
d
t
=
π
∫
0
1
(
x
−
x
2
2
)
2
⋅
1
+
2
x
2
d
x
{\displaystyle V=\pi \int _{0}^{\sqrt {2}}{\overline {PH}}^{2}dt=\pi \int _{0}^{1}({\frac {x-x^{2}}{\sqrt {2}}})^{2}\cdot {\frac {1+2x}{\sqrt {2}}}dx}
=
π
2
2
∫
0
1
(
2
x
5
−
3
x
4
+
x
2
)
d
x
=
2
π
4
[
1
3
x
6
−
3
5
x
5
+
1
3
x
3
]
0
1
=
2
π
60
{\displaystyle ={\frac {\pi }{2{\sqrt {2}}}}\int _{0}^{1}(2x^{5}-3x^{4}+x^{2})dx={\frac {{\sqrt {2}}\pi }{4}}[{\frac {1}{3}}x^{6}-{\frac {3}{5}}x^{5}+{\frac {1}{3}}x^{3}]_{0}^{1}={\frac {{\sqrt {2}}\pi }{60}}}
この解答を簡潔に纏めると、直線Lをt軸と見做してt軸についての回転体の式を立て、それをx軸についての回転体の式へと置換積分している。
①傘型分割積分
上の例題で考えると、長さ
P
Q
¯
{\displaystyle {\overline {PQ}}}
Δ
x
{\displaystyle \Delta x}
傘型分割積分 という。不足なく論理展開を記述できれば、入試でこの考え方を用いても減点される可能性は低いだろう。
この過程を一般化すると、以下の公式を導くことができる。
曲線
y
=
f
(
x
)
{\displaystyle y=f(x)}
m
x
+
n
,
x
=
a
,
x
=
b
{\displaystyle mx+n,x=a,x=b}
y
=
m
x
+
n
{\displaystyle y=mx+n}
V
=
π
cos
θ
∫
a
b
{
f
(
x
)
−
(
m
x
+
n
)
}
2
d
x
{\displaystyle V=\pi \cos \theta \int _{a}^{b}\{f(x)-(mx+n)\}^{2}dx}
ただし、
tan
θ
=
m
{\displaystyle \tan \theta =m}
この公式は完全に裏技なので、記述問題では(証明なしに)使用しない方が無難である。
図形全体を回転移動することにより、回転軸をx軸(もしくはy軸)に重ねることで、強引に回転体の公式に代入する方法。
回転移動には複素数平面の知識 、行列の知識 のどちらを用いても良い。
この方法では、回転後の図形の方程式が媒介変数表示で出現する場合がある。その場合、回転体の公式を媒介変数についての積分へと置換積分すれば良い。
曲線
{
x
=
f
(
t
)
y
=
g
(
t
)
{\displaystyle {\begin{cases}x=f(t)\\y=g(t)\end{cases}}}
f
(
t
)
,
g
(
t
)
{\displaystyle f(t),g(t)}
a
≦
t
≦
b
{\displaystyle a\leqq t\leqq b}
[
a
,
t
]
{\displaystyle [a,t]}
s
(
t
)
{\displaystyle s(t)}
t
{\displaystyle t}
Δ
t
{\displaystyle \Delta t}
Δ
s
≒
(
Δ
x
)
2
+
(
Δ
y
)
2
{\displaystyle \Delta s\fallingdotseq {\sqrt {(\Delta x)^{2}+(\Delta y)^{2}}}}
Δ
s
Δ
t
=
(
Δ
x
Δ
t
)
2
+
(
Δ
y
Δ
t
)
2
{\displaystyle {\frac {\Delta s}{\Delta t}}={\sqrt {({\frac {\Delta x}{\Delta t}})^{2}+({\frac {\Delta y}{\Delta t}})^{2}}}}
Δ
t
→
0
{\displaystyle \Delta t\to 0}
d
s
d
t
=
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
{\displaystyle {\frac {ds}{dt}}={\sqrt {({\frac {dx}{dt}})^{2}+({\frac {dy}{dt}})^{2}}}}
この微分方程式を解くと、
d
s
=
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
d
t
{\displaystyle ds={\sqrt {({\frac {dx}{dt}})^{2}+({\frac {dy}{dt}})^{2}}}dt}
∫
d
s
=
∫
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
d
t
{\displaystyle \int ds=\int {\sqrt {({\frac {dx}{dt}})^{2}+({\frac {dy}{dt}})^{2}}}dt}
s
=
∫
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
d
t
+
C
{\displaystyle s=\int {\sqrt {({\frac {dx}{dt}})^{2}+({\frac {dy}{dt}})^{2}}}dt+C}
ここで
s
(
t
)
{\displaystyle s(t)}
s
(
b
)
−
s
(
a
)
=
∫
a
b
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
d
t
{\displaystyle s(b)-s(a)=\int _{a}^{b}{\sqrt {({\frac {dx}{dt}})^{2}+({\frac {dy}{dt}})^{2}}}dt}
よって、以下のようになる。
曲線の長さ(Ⅰ)
曲線
{
x
=
f
(
t
)
y
=
g
(
t
)
{\displaystyle {\begin{cases}x=f(t)\\y=g(t)\end{cases}}}
[
a
,
b
]
{\displaystyle [a,b]}
L
=
∫
a
b
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
d
t
{\displaystyle L=\int _{a}^{b}{\sqrt {({\frac {dx}{dt}})^{2}+({\frac {dy}{dt}})^{2}}}dt}
y
=
f
(
x
)
{\displaystyle y=f(x)}
{
x
=
t
y
=
f
(
t
)
{\displaystyle {\begin{cases}x=t\\y=f(t)\end{cases}}}
曲線の長さ(Ⅱ)
曲線
y
=
f
(
x
)
{\displaystyle y=f(x)}
[
a
,
b
]
{\displaystyle [a,b]}
L
=
∫
a
b
1
+
(
d
y
d
x
)
2
d
t
{\displaystyle L=\int _{a}^{b}{\sqrt {1+({\frac {dy}{dx}})^{2}}}dt}
微分法で学んだ ように、数直線上を運動する点Pの時刻tにおける位置,速度がそれぞれ
x
(
t
)
,
v
(
t
)
{\displaystyle x(t),v(t)}
v
(
t
)
=
d
d
t
x
(
t
)
{\displaystyle v(t)={\frac {d}{dt}}x(t)}
x
(
t
)
=
∫
v
(
t
)
d
t
+
C
{\displaystyle x(t)=\int v(t)dt+C}
x
0
{\displaystyle x_{0}}
点Pが
t
=
a
{\displaystyle t=a}
t
=
b
{\displaystyle t=b}
x
(
b
)
−
x
(
a
)
=
∫
a
b
v
(
t
)
d
t
{\displaystyle x(b)-x(a)=\int _{a}^{b}v(t)dt}
x
(
b
)
=
x
(
a
)
+
∫
a
b
v
(
t
)
d
t
{\displaystyle x(b)=x(a)+\int _{a}^{b}v(t)dt}
x
(
a
)
{\displaystyle x(a)}
x
0
{\displaystyle x_{0}}
また、上の場合において道のりは
∫
a
b
|
v
(
t
)
|
d
t
{\displaystyle \int _{a}^{b}|v(t)|dt}
x
(
t
)
≧
0
{\displaystyle x(t)\geqq 0}
平面上の運動も同様である。
なお、加速度は位置の二階微分なので、加速度を二階積分すれば位置が求まる。よって、時刻tにおける加速度が
a
(
t
)
=
a
{\displaystyle a(t)=a}
x
(
t
)
=
∫
∫
a
(
t
)
d
t
d
t
=
∫
(
a
t
+
v
0
)
d
t
=
1
2
a
t
2
+
v
0
t
+
x
0
{\displaystyle x(t)=\int \!\int a(t)dt\;dt=\int (at+v_{0})dt={\frac {1}{2}}at^{2}+v_{0}t+x_{0}}
等加速度直線運動 の式)
ベクトル関数
変数tの値を決めるとベクトルA(t)の値が一意に定まるとき、A(t)をtの
ベクトル関数 という。基本ベクトルを用いると、ベクトル関数は基本ベクトルのスカラー倍の足し算に分解することができる。このとき、基本ベクトルにかかる係数をベクトル関数の
成分 という。ベクトル関数の定義より、成分はtの関数になる。
つまり、ベクトル関数に関する微積分はその成分をそれぞれ微分/積分すれば良い ということがわかる。
例えば、速度を表すベクトル関数
v
→
(
t
)
=
(
2
t
3
t
2
−
1
)
{\displaystyle {\vec {v}}(t)={\begin{pmatrix}2t\\3t^{2}-1\end{pmatrix}}}
(
x
0
y
0
)
=
(
0
0
)
{\displaystyle {\begin{pmatrix}x_{0}\\y_{0}\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}}
x
→
(
t
)
=
∫
v
→
(
t
)
d
t
=
(
∫
(
2
t
)
d
t
∫
(
3
t
2
−
1
)
d
t
)
=
(
t
2
t
3
−
t
)
{\displaystyle {\vec {x}}(t)=\int {\vec {v}}(t)dt={\begin{pmatrix}\int (2t)dt\\\int (3t^{2}-1)dt\end{pmatrix}}={\begin{pmatrix}t^{2}\\t^{3}-t\end{pmatrix}}}
a
→
(
t
)
=
d
d
t
v
→
(
t
)
=
(
d
d
t
(
2
t
)
d
d
t
(
3
t
2
−
1
)
)
=
(
2
6
t
)
{\displaystyle {\vec {a}}(t)={\frac {d}{dt}}{\vec {v}}(t)={\begin{pmatrix}{\frac {d}{dt}}(2t)\\{\frac {d}{dt}}(3t^{2}-1)\end{pmatrix}}={\begin{pmatrix}2\\6t\end{pmatrix}}}
t
=
0
{\displaystyle t=0}
t
=
2
{\displaystyle t=2}
構文解析失敗 (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Bracket argument to \\ must be a dimension"): {\displaystyle {\begin{pmatrix}\Delta x\\\Delta y\end{pmatrix}}=\int _{0}^{2}{\vec {v}}(t)dt={\begin{pmatrix}\int _{0}^{2}(2t)dt\\\int _{0}^{2}(3t^{2}-1)dt\end{pmatrix}}={\begin{pmatrix}[t^{2}]_{0}^{2}\\[t^{3}-t]_{0}^{2}\end{pmatrix}}={\begin{pmatrix}4\\6\end{pmatrix}}}
と求まる 。
すなわち、速度・加速度・位置・道のり等に関する問題はベクトル関数の微積分を計算する問題であると言える。
これまでに学んだように、積分は微分の逆演算であると同時に、座標平面上での面積計算でもある。この項では、座標平面上の面積計算の方法の一つである区分求積法、および積分法との関連について学ぶ。
面積計算 右図のようなある曲線
y
=
f
(
x
)
{\displaystyle y=f(x)}
f
(
x
)
>
0
{\displaystyle f(x)>0}
x 軸、および直線
x
=
a
,
x
=
b
(
a
<
b
)
{\displaystyle x=a,x=b(a<b)}
S を求める。この面積は#面積 の項で学んだように、
S
=
∫
a
b
f
(
x
)
d
x
{\displaystyle S=\int _{a}^{b}f(x)dx}
と積分法を用いて計算することができた。では、これをもう少し原始的な方法で近似的に求めることを考えてみよう。
曲線を含む図形の面積を求めることは簡単ではないが、例えば三角形や長方形、台形などの直線で囲まれた図形の面積を求めることは難しくない。そこで、下図のようにy=f(x)を棒グラフで近似し、長方形の面積の和を計算することで、求めたい面積S に近い値を求めることができる。左下のように棒グラフの幅が大きいと誤差も大きいが、棒グラフの幅を狭くすればするほど、すなわち分割数を多くするほど、徐々に求めたい面積の値に近づけることができる。そこで、この区間[a ,b ]をn 等分し、その時の長方形の面積の総和を求め、その後で
n
→
∞
{\displaystyle n\to \infty }
区分求積法 と呼ぶ。
左側で近似 右側で近似
y
=
f
(
x
)
{\displaystyle y=f(x)}
ここでは面積を求めたい区間を、単純のため[0, 1]とする。区間[0, 1]をn 等分するとき、それぞれの長方形の左端のx座標は、
0
,
1
n
,
2
n
,
⋯
,
n
−
1
n
{\displaystyle 0,{\frac {1}{n}},{\frac {2}{n}},\cdots ,{\frac {n-1}{n}}}
となる。ここで、一般に第k 番目の長方形について考えることにする。ただし、いちばん左側の長方形を第0番目とし、いちばん右側の長方形を第n -1番目とする。第k 番目の長方形の左端のx座標は
k
n
{\displaystyle {\frac {k}{n}}}
f
(
k
n
)
{\displaystyle f\left({\frac {k}{n}}\right)}
1
n
{\displaystyle {\frac {1}{n}}}
s
k
{\displaystyle s_{k}}
s
k
=
1
n
f
(
k
n
)
{\displaystyle s_{k}={\frac {1}{n}}f\left({\frac {k}{n}}\right)}
となる。したがって、これらの長方形の面積の総和
S
n
{\displaystyle S_{n}}
S
n
=
∑
k
=
0
n
−
1
s
k
=
1
n
∑
k
=
0
n
−
1
f
(
k
n
)
{\displaystyle S_{n}=\sum _{k=0}^{n-1}s_{k}={\frac {1}{n}}\sum _{k=0}^{n-1}f\left({\frac {k}{n}}\right)}
この
S
n
{\displaystyle S_{n}}
n 等分した時の長方形の面積の総和であるが、n を大きくすればするほど、次第にもとの面積に近づいていく。したがって、
n
→
∞
{\displaystyle n\to \infty }
S
=
lim
n
→
∞
S
n
=
lim
n
→
∞
1
n
∑
k
=
0
n
−
1
f
(
k
n
)
{\displaystyle S=\lim _{n\to \infty }S_{n}=\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=0}^{n-1}f\left({\frac {k}{n}}\right)}
となる。このようにして、求めたい面積を計算することができる。さらに、ここでこの区間の面積が積分法により計算できたことから、
lim
n
→
∞
1
n
∑
k
=
0
n
−
1
f
(
k
n
)
=
∫
0
1
f
(
x
)
d
x
{\displaystyle \lim _{n\to \infty }{\frac {1}{n}}\sum _{k=0}^{n-1}f\left({\frac {k}{n}}\right)=\int _{0}^{1}f(x)dx}
が成り立つ。また、長方形の右上の頂点を曲線上に取る場合は、同様にして
S
=
lim
n
→
∞
1
n
∑
k
=
1
n
f
(
k
n
)
=
∫
0
1
f
(
x
)
d
x
{\displaystyle S=\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=1}^{n}f\left({\frac {k}{n}}\right)=\int _{0}^{1}f(x)dx}
となる。
シグマの範囲の有限個のズレは無視して良い 。nを無限大に飛ばした極限を考えるとき、有限個あるズレの値は全て0に収束するからである。
lim
n
→
∞
1
n
∑
k
=
l
n
−
m
f
(
k
n
)
=
∫
0
1
f
(
x
)
d
x
{\displaystyle \lim _{n\to \infty }{\frac {1}{n}}\sum _{k=l}^{n-m}f\left({\frac {k}{n}}\right)=\int _{0}^{1}f(x)dx}
∫
a
b
f
(
x
)
d
x
=
lim
n
→
∞
∑
k
=
l
n
−
m
f
(
x
k
)
Δ
x
{\displaystyle \int _{a}^{b}f(x)dx=\lim _{n\to \infty }\sum _{k=l}^{n-m}f(x_{k})\Delta x}
ただし、
Δ
x
=
b
−
a
n
,
x
k
=
a
+
k
Δ
x
{\displaystyle \Delta x={\frac {b-a}{n}},x_{k}=a+k\Delta x}
証明は先ほどと同様である。リーマン和 という)の極限とする場合がある。数学Ⅱで扱った微分積分学の基本定理は、リーマン和(面積計算)と原始関数(微分の逆演算)という二つの概念を結びつけている定理であると言える。
なお、
lim
n
→
∞
∑
k
=
a
n
+
l
b
n
−
m
f
(
k
n
)
=
∫
a
b
f
(
x
)
d
x
{\displaystyle \lim _{n\to \infty }\sum _{k=an+l}^{bn-m}f\left({\frac {k}{n}}\right)=\int _{a}^{b}f(x)dx}
^ 右辺が0のとき双曲線とはならないが、このときは簡単に平方根を外すことが出来るので考える必要はない。
^ なお、この時、
d
t
{\displaystyle dt}
S
(
t
)
{\displaystyle S(t)}
^ 三角錐
O
−
A
B
C
{\displaystyle O-ABC}
△
A
B
C
{\displaystyle \triangle {ABC}}
S
=
1
{\displaystyle S=1}
O
A
{\displaystyle OA}
1
{\displaystyle 1}
1
3
{\displaystyle {\frac {1}{3}}}
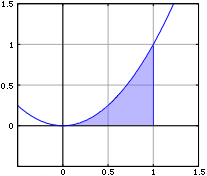


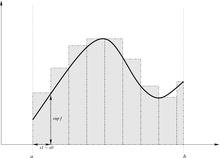


















































































































































![{\displaystyle [\alpha ,\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/878fce9eb3ba664f0ad4d025f04214fa85ee9583)



![{\displaystyle \int _{a}^{b}f(x)g'(x)\,dx=\left[f(x)g(x)\right]_{b}^{a}-\int _{a}^{b}f'(x)g(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8f6487246f687afe441baaeafb2005152992aab)
















![{\displaystyle \left[{\frac {a+b}{2}},b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5cd05ef535fe28124252885904819a07c058d8e)


![{\displaystyle \left[a,{\frac {a+b}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2340575cf6aac755487555f6b71544a147ad4381)



![{\displaystyle \int _{a}^{b}f(x)\,dx=\int _{a}^{\frac {a+b}{2}}f(x)\,dx+\int _{\frac {a+b}{2}}^{b}f(x)\,dx=\int _{a}^{\frac {a+b}{2}}[f(x)+f(a+b-x)]\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c0c0f87859928d0724ba4c2ddefdabaf5e7472d)

![{\displaystyle {\begin{aligned}\int _{0}^{\frac {\pi }{2}}{\frac {\sin x}{\sin x+\cos x}}\,dx&=\int _{0}^{\frac {\pi }{4}}\left[{\frac {\sin x}{\sin x+\cos x}}+{\frac {\sin({\frac {\pi }{2}}-x)}{\sin({\frac {\pi }{2}}-x)+\cos({\frac {\pi }{2}}-x)}}\right]\,dx\\&=\int _{0}^{\frac {\pi }{4}}\left[{\frac {\sin x}{\sin x+\cos x}}+{\frac {\cos x}{\cos x+\sin x}}\right]\,dx\\&=\int _{0}^{\frac {\pi }{4}}dx={\frac {\pi }{4}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cf9bf40bc058942b7bacf67d4fce6d719563dfb)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









![{\displaystyle =\sum _{k=1}^{n}\int _{k}^{k+1}{\frac {dx}{x}}=\int _{1}^{n+1}{\frac {dx}{x}}=\left[\log(x)\right]_{1}^{n+1}=\log(n+1)-\log(1)=\log(n+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15343aefcd62f8ee9885c693d73cdf60be61de16)










































![{\displaystyle [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)














![{\displaystyle [\tau ,\tau +\Delta \tau ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1eb905b81037c255a75c3e5b93afd5b9667602)































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle V=\int _{0}^{1}S(t)\,dt=\int _{0}^{1}t^{2}\,dt=\left[{\frac {t^{3}}{3}}\right]_{0}^{1}={\frac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4955b7a228713dc204043f96fbe4f93f279cb055)












![{\displaystyle V=\int _{0}^{1}S(t)\,dt=\int _{0}^{1}(2t^{2}-2t+1)\,dt=\left[{\frac {2t^{3}}{3}}-t^{2}+t\right]_{0}^{1}={\frac {2}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b2a52b2f3a3f6b21ca42c9e04e43cdbc54f1195)
















}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fef9e48957054ad786fb42e0b05e1f96e01d4bc9)



















![{\displaystyle ={\frac {\pi }{2{\sqrt {2}}}}\int _{0}^{1}(2x^{5}-3x^{4}+x^{2})dx={\frac {{\sqrt {2}}\pi }{4}}[{\frac {1}{3}}x^{6}-{\frac {3}{5}}x^{5}+{\frac {1}{3}}x^{3}]_{0}^{1}={\frac {{\sqrt {2}}\pi }{60}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc0036e6a207cf6be6efcf5852113aca56c5a71b)








![{\displaystyle [a,t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7e4d6424116f83d1d8eadea305b1ccc9c8744e)

























































