本項は高等学校数学A の「数学と人間の活動」の解説です。
第1節「数量や図形の概念と人間の活動」では、前課程数学A「整数の性質」 の内容の一部と図形の活用について学びます。
第2節「数学と文化」では、数学史とそれに関連した内容・ゲームやパズルの中の数学について学びます。 数学A「場合の数と確率 」及び数学I「三角比 」の履修後に学習してください。
∧
{\displaystyle \land }
且つ ( かつ ) 論理記号 です。
0に1を足し引きして求められる数を整数 という。
特に、正の整数1, 2, 3,・・・を自然数 という。
自然数は、人間が生活する上で自然に登場した数であることからその名前がついた。
自然数に0を含めたものを非負整数 という。
正整数 と呼んで区別する。
a
,
b
{\displaystyle a,b}
a
=
k
b
{\displaystyle a=kb}
k
{\displaystyle k}
a
{\displaystyle a}
b
{\displaystyle b}
倍数 である」「
b
{\displaystyle b}
a
{\displaystyle a}
約数 である」といい、
b
|
a
{\displaystyle b|a}
a
=
k
b
{\displaystyle a=kb}
a
=
(
−
b
)
(
−
k
)
{\displaystyle a=(-b)(-k)}
b
|
a
{\displaystyle b|a}
−
b
|
a
{\displaystyle -b|a}
a
|
b
{\displaystyle a|b}
b
|
a
{\displaystyle b|a}
a
=
b
{\displaystyle a=b}
また、0は全ての整数の倍数であり、1は全ての整数の約数である。
2の倍数を偶数 、偶数ではない整数を奇数 という。
任意の自然数をnとすると、
nの一の位が偶数ならば2|n
nの各位の数の和が3の倍数ならば3|n
nの下二桁が4の倍数ならば4|n
nの一の位が0または5ならば5|n
nの下三桁が8の倍数ならば8|n
nの各位の数の和が9の倍数ならば9|n
nの一の位が0ならば10|n
nの各桁を一桁ずつ交互に足し引きした数が11の倍数ならば11|n 負の整数についても、その絶対値を考えることで上の判定法を適用できる。
なお、11|nならば、nの各桁の並べ方を反転させた数も11の倍数であることが知られている。(例:132=11×12, 231=11×21)
問題
四桁の自然数Nについて、上の判定法が正しいことを証明せよ。
7の倍数の判定法を一つ作れ。
バーコードの仕組み
バーコードの13桁の数字について、(左から奇数桁目の数の和)+(左から偶数桁目の数の和)×3が必ず10の倍数となる。
左から十二桁目までの数字は商品ごとに振られたものであるが、最後の十三桁目の数字は、上の計算結果が10の倍数になるように振られている。
機械で読み取った結果10の倍数にならなかったら、読み取りミスがあったと判定するのである。
2以上の自然数で、1とその数自身以外に正の約数をもたないものを素数 という。2ではない素数を特に奇素数 という。2以上の自然数で素数ではないものを合成数 という。1は素数でも合成数でもなく、全ての整数の約数であることから乗法単位元 と呼ばれる。なお、0は加法単位元 と呼ばれる。
エラトステネスの篩 ( ふるい )
[1] 自然数を1から順番に並べた表を作る(並べる自然数の数はいくらでも良い)
[2] 1に斜線を引く
[3] 2に○を付け、以降の2の倍数に全て斜線を引く
[4] ○も斜線もついていない最小の数である3に○をつけ、以降の3の倍数に全て斜線を引く
[5] 以後、表の全ての数に○と斜線がつくまで繰り返し、○が付いた数が求める素数である。
この方法を用いると、確実に全ての素数を網羅できる。ただし、大きな素数を求めるためにはコンピュータの力を借りる必要がある。
因数 という。
素数である因数を素因数 といい、自然数を素数だけの積で表すことを素因数分解 という。
100を素因数分解せよ。
100
=
10
×
10
=
2
×
5
×
2
×
5
=
2
2
5
2
{\displaystyle 100=10\times 10=2\times 5\times 2\times 5=2^{2}5^{2}}
素因数分解の一意性 という。
1を素数に含まないのは、素因数分解の一意性を成り立たせるためである。もし1を素数に含めると、1を何回かけても値は変わらないので、例えば6の素因数分解を答えるときに2×3, 2×3×1, 2×3×1×1, …と表し方が無限に存在してしまう。また、エラトステネスの篩を用いようとすると、1に丸をつけると以降の数は全て1を因数に持つため斜線を引けてしまい、「素数は1のみである」という誤った結論が出てしまう。このような不都合を無くすため、1は素数に含まれていない。
問題
次の数を素因数分解せよ。
98
225
1024
16534
136578
RSA暗号
上の問題から分かるように、一般に数が大きければ大きくなるほど、素因数分解は困難になる。逆に、数が大きくても素因数の積を求めることはそこまで難しくない。
この性質を利用したのが、RSA暗号である。
RSA暗号では、巨大な数を2つの素数の積に分解することが暗号を解く鍵の役割を担い、その難しさが通信の安全性に繫がっている。
(詳しい仕組みについてはこのページの内容を全て修得した後にw:RSA暗号 を参照してほしい。)
しかし、量子コンピュータが実現すれば、RSA暗号ですらも容易に破られてしまうと言われている。
そのため、RSA暗号よりも強力な暗号方式が模索されている。
自然数Nの素因数分解が
N
=
p
a
q
b
r
c
⋯
{\displaystyle N=p^{a}q^{b}r^{c}\cdots }
p
{\displaystyle p}
a
+
1
{\displaystyle a+1}
q
{\displaystyle q}
b
+
1
{\displaystyle b+1}
r
{\displaystyle r}
c
+
1
{\displaystyle c+1}
(
a
+
1
)
(
b
+
1
)
(
c
+
1
)
⋯
{\displaystyle (a+1)(b+1)(c+1)\cdots }
約数の個数
自然数Nの素因数分解が
N
=
p
a
q
b
r
c
⋯
{\displaystyle N=p^{a}q^{b}r^{c}\cdots }
(
a
+
1
)
(
b
+
1
)
(
c
+
1
)
⋯
{\displaystyle (a+1)(b+1)(c+1)\cdots }
約数の総和
自然数Nの素因数分解が
N
=
p
a
q
b
r
c
⋯
{\displaystyle N=p^{a}q^{b}r^{c}\cdots }
(
1
+
p
+
p
2
+
⋯
+
p
a
)
(
1
+
q
+
q
2
+
⋯
+
q
b
)
(
1
+
r
+
r
2
+
⋯
+
r
c
)
⋯
{\displaystyle (1+p+p^{2}+\cdots +p^{a})(1+q+q^{2}+\cdots +q^{b})(1+r+r^{2}+\cdots +r^{c})\cdots }
例えば、6の正の約数は1, 2, 3, 6なので、これを全て足すと12である。6を素因数分解すると2×3なので、上の公式に代入すると(1+2)×(1+3)=3×4=12と、一致することが確かめられた。
三角関数 を用いた以下の式が存在する。
∑
s
=
1
n
∑
t
=
1
s
cos
2
π
t
n
s
{\displaystyle \sum _{s=1}^{n}\sum _{t=1}^{s}\cos {\frac {2\pi tn}{s}}}
記号
∑
k
=
1
n
{\displaystyle \sum _{k=1}^{n}}
こちら を参照。
この式は見た目こそ美しいが、実際に計算するにはコサインの値を
∑
k
=
1
n
k
(
=
n
(
n
−
1
)
2
)
{\displaystyle \sum _{k=1}^{n}k(={\frac {n(n-1)}{2}})}
2つ以上の整数に共通な倍数をそれらの整数の公倍数 といい、正の公倍数で最小であるものを最小公倍数 という。
a
,
b
,
c
,
⋯
{\displaystyle a,b,c,\cdots }
l
c
m
(
a
,
b
,
c
,
⋯
)
{\displaystyle \mathrm {lcm} (a,b,c,\cdots )}
l
c
m
(
100
,
35
,
3
)
{\displaystyle \mathrm {lcm} (100,35,3)}
100
=
2
2
5
2
,
35
=
5
1
7
1
,
3
=
3
1
{\displaystyle 100=2^{2}5^{2},35=5^{1}7^{1},3=3^{1}}
2
2
3
1
5
2
7
1
=
2100
{\displaystyle 2^{2}3^{1}5^{2}7^{1}=2100}
a
{\displaystyle a}
b
{\displaystyle b}
l
c
m
(
a
,
b
)
{\displaystyle \mathrm {lcm} (a,b)}
問題
自然数
k
{\displaystyle k}
n
|
(
k
−
1
)
k
(
k
+
1
)
{\displaystyle n|(k-1)k(k+1)}
n
{\displaystyle n}
彗星Aが太陽に最接近する周期が17年、彗星Bが太陽に最接近する周期が330年、彗星Cが太陽に最接近する周期が2000年であるという。3つの彗星が同じ年に太陽に再接近したとき、次に3つの彗星が同じ年に太陽に最接近するのは何年後であるか答えよ。
干支
子 ( ね ) 丑 ( うし ) 寅 ( とら ) 卯 ( う ) 辰 ( たつ ) 巳 ( み ) 午 ( うま ) 未 ( ひつじ ) 申 ( さる ) 酉 ( とり ) 戌 ( いぬ ) 亥 ( い ) 十二支 ( じゅうにし ) 甲 ( きのえ ) 乙 ( きのと ) 丙 ( ひのえ ) 丁 ( ひのと ) 戊 ( つちのえ ) 己 ( つちのと ) 庚 ( かのえ ) 辛 ( かのと ) 壬 ( みずのえ ) 癸 ( みずのと ) 十干 ( じっかん ) 干支 ( えと )
その名の如く、十二支は12年周期、十干は10年周期である。それでは、干支の周期は何年であろうか?最小公倍数の考えを用いて求めてみよう。
12
=
2
2
3
1
,
10
=
2
1
5
1
{\displaystyle 12=2^{2}3^{1},10=2^{1}5^{1}}
l
c
m
(
12
,
10
)
=
2
2
3
1
5
1
=
60
{\displaystyle \mathrm {lcm} (12,10)=2^{2}3^{1}5^{1}=60}
例えば、初の東京オリンピックが開催された1964年の干支は「甲辰」であることから、2024年の干支は「甲辰」であるとわかる。
日本では60歳のことを「還暦 ( かんれき )
なお、120歳のことは「大還暦」と呼ぶが、執筆時点の日本最高齢記録は119歳なので、未だ大還暦を祝われた人はいない。(2024年現在認定されている世界記録は122歳だが正確性に疑問が持たれているため、もしかしたら未だ人類で大還暦に到達した人はいないかもしれない。)
公約数 といい、正の公約数で最大であるものを最大公約数 という。
a
,
b
,
c
,
⋯
{\displaystyle a,b,c,\cdots }
g
c
d
(
a
,
b
,
c
,
⋯
)
{\displaystyle \mathrm {gcd} (a,b,c,\cdots )}
g
c
d
(
252
,
300
,
420
)
{\displaystyle \mathrm {gcd} (252,300,420)}
252
=
2
2
3
2
7
1
,
300
=
2
2
3
1
5
2
,
420
=
2
2
3
1
5
1
7
1
{\displaystyle 252=2^{2}3^{2}7^{1},300=2^{2}3^{1}5^{2},420=2^{2}3^{1}5^{1}7^{1}}
2
2
3
1
5
0
7
0
=
12
{\displaystyle 2^{2}3^{1}5^{0}7^{0}=12}
互いに素 という。
このページでは
a
{\displaystyle a}
b
{\displaystyle b}
a
⊥
b
{\displaystyle a\perp b}
a
,
b
,
c
,
⋯
{\displaystyle a,b,c,\cdots }
g
c
d
(
a
,
b
,
c
,
⋯
)
=
1
{\displaystyle \mathrm {gcd} (a,b,c,\cdots )=1}
a
⊥
b
∧
b
⊥
c
∧
c
⊥
a
∧
⋯
{\displaystyle a\perp b\land b\perp c\land c\perp a\land \cdots }
対ごとに素 という。
互いに素である確率
s
{\displaystyle s}
リーマンのゼータ関数 を用いて以下のように表される。
p
=
1
ζ
(
s
)
{\displaystyle p={\frac {1}{\zeta (s)}}}
ただし、
ζ
(
s
)
=
lim
n
→
∞
∑
k
=
1
n
1
k
s
=
1
+
1
2
s
+
1
3
s
+
⋯
+
1
n
s
+
⋯
{\displaystyle \zeta (s)=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {1}{k^{s}}}=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots +{\frac {1}{n^{s}}}+\cdots }
記号
∑
k
=
1
n
{\displaystyle \sum _{k=1}^{n}}
こちら 、
lim
n
→
∞
{\displaystyle \lim _{n\to \infty }}
こちら を参照。
s
{\displaystyle s}
ζ
(
s
)
{\displaystyle \zeta (s)}
π
{\displaystyle \pi }
例えば、
ζ
(
2
)
=
π
2
6
{\displaystyle \zeta (2)={\frac {\pi ^{2}}{6}}}
つまり、ランダムに選んだ2つの整数が互いに素である確率は
6
π
2
≒
60.8
%
{\displaystyle {\frac {6}{\pi ^{2}}}\fallingdotseq 60.8\%}
分配法則
l
c
m
(
a
,
b
,
c
)
=
l
c
m
(
l
c
m
(
a
,
b
)
,
c
)
=
l
c
m
(
a
,
l
c
m
(
b
,
c
)
)
{\displaystyle \mathrm {lcm} (a,b,c)=\mathrm {lcm} (\mathrm {lcm} (a,b),c)=\mathrm {lcm} (a,\mathrm {lcm} (b,c))}
g
c
d
(
a
,
b
,
c
)
=
g
c
d
(
g
c
d
(
a
,
b
)
,
c
)
=
g
c
d
(
a
,
g
c
d
(
b
,
c
)
)
{\displaystyle \mathrm {gcd} (a,b,c)=\mathrm {gcd} (\mathrm {gcd} (a,b),c)=\mathrm {gcd} (a,\mathrm {gcd} (b,c))}
最小公倍数と最大公約数の関係
l
c
m
(
a
,
b
)
=
g
c
d
(
a
,
b
)
α
β
{\displaystyle \mathrm {lcm} (a,b)=\mathrm {gcd} (a,b)\alpha \beta }
α
=
a
g
c
d
(
a
,
b
)
,
β
=
b
g
c
d
(
a
,
b
)
{\displaystyle \alpha ={\frac {a}{\mathrm {gcd} (a,b)}},\beta ={\frac {b}{\mathrm {gcd} (a,b)}}}
l
c
m
(
a
,
b
)
g
c
d
(
a
,
b
)
=
a
b
{\displaystyle \mathrm {lcm} (a,b)\mathrm {gcd} (a,b)=ab}
一番下の式は最大公約数が計算しにくい場合に使われるが、3つ以上の整数の場合には使えない 。
自然数の割り算は小学校で扱った。ここでは、整数の割り算と余りについて考える。
整数の割り算
整数
a
{\displaystyle a}
正整数
b
{\displaystyle b}
a
=
b
q
+
r
{\displaystyle a=bq+r}
q
,
r
{\displaystyle q,r}
0
≦
r
<
b
{\displaystyle 0\leqq r<b}
q
{\displaystyle q}
商 、
r
{\displaystyle r}
余り という。
r
=
0
{\displaystyle r=0}
a
{\displaystyle a}
b
{\displaystyle b}
割り切れる 」といい、
r
≠
0
{\displaystyle r\neq 0}
割り切れない 」という。
余りの性質
2つの整数
a
,
b
{\displaystyle a,b}
p
{\displaystyle p}
m
,
n
{\displaystyle m,n}
a
±
b
{\displaystyle a\pm b}
p
{\displaystyle p}
m
±
n
{\displaystyle m\pm n}
p
{\displaystyle p}
a
b
{\displaystyle ab}
p
{\displaystyle p}
m
n
{\displaystyle mn}
p
{\displaystyle p}
a
b
{\displaystyle a^{b}}
p
{\displaystyle p}
m
b
{\displaystyle m^{b}}
p
{\displaystyle p}
問題
「私の年齢を3で割った余りは2、5で割った余りは3、7で割った余りは4である。私の年齢は何歳か。ただし、105歳より下である。」という問題について、以下の問いに答えよ
70
×
2
+
21
×
3
+
15
×
4
{\displaystyle 70\times 2+21\times 3+15\times 4}
上の式の
70
,
21
,
15
{\displaystyle 70,21,15}
上の問題は江戸時代の数学書『塵劫記』に載っているもので、1番の問題で確かめた解法は百五減算 と呼ばれている。百五減算にはw:中国剰余定理 が利用されている。
ユークリッドの互除法 とは、素因数分解が容易ではない場合に最大公約数を求める方法である。
a
,
b
{\displaystyle a,b}
a
=
b
k
+
r
{\displaystyle a=bk+r}
k
,
r
{\displaystyle k,r}
r
=
0
{\displaystyle r=0}
b
=
r
l
+
s
{\displaystyle b=rl+s}
l
,
s
{\displaystyle l,s}
s
=
0
{\displaystyle s=0}
以下、余りが0になるまで繰り返す
余りが0になったときの割る数が求める最大公約数である。 整数の割り算の定義より、手順を繰り返すと余りは必ず小さくなり、余りは負にならないので、手順を有限回繰り替えせば必ず余りは0になり、最大公約数を見つけられる。
g
c
d
(
1071
,
1029
)
{\displaystyle \mathrm {gcd} (1071,1029)}
1071
=
1029
×
1
+
42
{\displaystyle 1071=1029\times 1+42}
1029
=
42
×
24
+
21
{\displaystyle 1029=42\times 24+21}
42
=
21
×
2
+
0
{\displaystyle 42=21\times 2+0}
よって、
g
c
d
(
1071
,
1029
)
=
21
{\displaystyle \mathrm {gcd} (1071,1029)=21}
互除法の原理
正整数
a
,
b
{\displaystyle a,b}
a
{\displaystyle a}
b
{\displaystyle b}
r
{\displaystyle r}
g
c
d
(
a
,
b
)
=
g
c
d
(
b
,
r
)
{\displaystyle \mathrm {gcd} (a,b)=\mathrm {gcd} (b,r)}
a
{\displaystyle a}
b
{\displaystyle b}
q
{\displaystyle q}
このとき、
a
=
b
q
+
r
{\displaystyle a=bq+r}
r
=
a
−
b
q
{\displaystyle r=a-bq}
g
c
d
(
a
,
b
)
=
m
,
g
c
d
(
b
,
r
)
=
n
{\displaystyle \mathrm {gcd} (a,b)=m,\mathrm {gcd} (b,r)=n}
m
|
r
{\displaystyle m|r}
m
{\displaystyle m}
b
{\displaystyle b}
r
{\displaystyle r}
m
≦
n
{\displaystyle m\leqq n}
一方、
n
|
a
{\displaystyle n|a}
n
{\displaystyle n}
b
{\displaystyle b}
a
{\displaystyle a}
n
≦
m
{\displaystyle n\leqq m}
よって、
n
≦
m
≦
n
{\displaystyle n\leqq m\leqq n}
m
=
n
{\displaystyle m=n}
問題
以下をユークリッドの互除法を用いて求めよ。
g
c
d
(
722
,
171
)
{\displaystyle \mathrm {gcd} (722,171)}
g
c
d
(
343
,
336
)
{\displaystyle \mathrm {gcd} (343,336)}
g
c
d
(
551
,
817
)
{\displaystyle \mathrm {gcd} (551,817)}
a
⊥
b
{\displaystyle a\perp b}
4
a
+
9
b
3
a
+
7
b
{\displaystyle {\frac {4a+9b}{3a+7b}}}
a
,
b
{\displaystyle a,b}
g
c
d
(
a
,
b
)
{\displaystyle \mathrm {gcd} (a,b)}
2辺の長さが有理数
p
,
q
{\displaystyle p,q}
k
p
,
k
q
{\displaystyle kp,kq}
k
{\displaystyle k}
2辺の長さのうち片方が無理数であれば、敷き詰める課程で元の長方形と相似な長方形が出現し、永遠に敷き詰めていっても隙間が埋まることはない。
問題
互除法を利用して
2
{\displaystyle {\sqrt {2}}}
ここでは、割り算の余りに関する表記簡略化のため、合同式 を導入する。
本来は大学の整数論 で扱う内容であるが、そこまで難しい内容ではなく、むしろ導入した方がこの先楽なので扱う。
a
,
b
{\displaystyle a,b}
m
{\displaystyle m}
a
{\displaystyle a}
b
{\displaystyle b}
m
{\displaystyle m}
法 として合同 である」といい、
a
≡
b
(
m
o
d
m
)
{\displaystyle a\equiv b(\mathrm {mod} ~m)}
合同式 という。
なお、
a
≡
b
(
m
o
d
m
)
⟺
m
|
(
a
−
b
)
{\displaystyle a\equiv b(\mathrm {mod} ~m)\iff m|(a-b)}
(
m
o
d
m
)
{\displaystyle (\mathrm {mod} ~m)}
m
{\displaystyle m}
m
{\displaystyle m}
a
≡
a
{\displaystyle a\equiv a}
a
≡
b
⟺
b
≡
a
{\displaystyle a\equiv b\iff b\equiv a}
a
≡
b
∧
b
≡
c
⟺
a
≡
c
{\displaystyle a\equiv b\land b\equiv c\iff a\equiv c}
k
{\displaystyle k}
m
{\displaystyle m}
a
≡
c
,
b
≡
d
{\displaystyle a\equiv c,b\equiv d}
a
±
b
≡
c
±
d
{\displaystyle a\pm b\equiv c\pm d}
a
b
≡
c
d
{\displaystyle ab\equiv cd}
a
k
≡
c
k
{\displaystyle a^{k}\equiv c^{k}}
整数係数多項式
f
(
x
)
{\displaystyle f(x)}
f
(
a
)
≡
f
(
b
)
{\displaystyle f(a)\equiv f(b)}
a
b
≡
a
c
(
m
o
d
m
)
∧
a
⊥
m
⟺
b
≡
c
(
m
o
d
m
)
{\displaystyle ab\equiv ac(\mathrm {mod} ~m)\land a\perp m\iff b\equiv c(\mathrm {mod} ~m)}
2
100
{\displaystyle 2^{100}}
7
{\displaystyle 7}
7
{\displaystyle 7}
2
3
≡
1
{\displaystyle 2^{3}\equiv 1}
2
100
≡
(
2
3
)
33
⋅
2
≡
1
33
⋅
2
≡
2
{\displaystyle 2^{100}\equiv (2^{3})^{33}\cdot 2\equiv 1^{33}\cdot 2\equiv 2}
故に、求める余りは
2
{\displaystyle 2}
問題
以下を求めよ
3
2222
{\displaystyle 3^{2222}}
5
{\displaystyle 5}
19
102
{\displaystyle 19^{102}}
n
2
≡
a
(
m
o
d
p
)
{\displaystyle n^{2}\equiv a(\mathrm {mod} ~p)}
a
{\displaystyle a}
p
{\displaystyle p}
平方剰余 である」といい、
(
a
p
)
=
1
{\displaystyle ({\dfrac {a}{p}})=1}
a
{\displaystyle a}
p
{\displaystyle p}
(
a
p
)
=
−
1
{\displaystyle ({\dfrac {a}{p}})=-1}
(
a
p
)
{\displaystyle ({\dfrac {a}{p}})}
ルジャンドル記号 という。
例えば、
n
=
1
,
p
=
3
{\displaystyle n=1,p=3}
1
2
≡
1
(
m
o
d
3
)
{\displaystyle 1^{2}\equiv 1(\mathrm {mod} ~3)}
(
1
3
)
=
1
{\displaystyle ({\dfrac {1}{3}})=1}
(
a
p
)
≡
a
p
−
1
2
(
m
o
d
p
)
∧
(
a
p
)
∈
{
−
1
,
0
,
1
}
{\displaystyle ({\dfrac {a}{p}})\equiv a^{\frac {p-1}{2}}(\mathrm {mod} ~p)\land ({\dfrac {a}{p}})\in \{-1,0,1\}}
(
2
3
)
=
−
1
{\displaystyle ({\dfrac {2}{3}})=-1}
3を法、
k
{\displaystyle k}
n
=
3
k
{\displaystyle n=3k}
n
2
=
9
k
2
≡
0
{\displaystyle n^{2}=9k^{2}\equiv 0}
n
=
3
k
+
1
{\displaystyle n=3k+1}
n
2
=
9
k
2
+
6
k
+
1
≡
1
{\displaystyle n^{2}=9k^{2}+6k+1\equiv 1}
n
=
3
k
+
2
{\displaystyle n=3k+2}
n
2
=
9
k
2
+
12
k
+
4
≡
1
{\displaystyle n^{2}=9k^{2}+12k+4\equiv 1}
よって、すべての場合において
n
2
{\displaystyle n^{2}}
法4における平方剰余は0,1の2種類だけであることを証明せよ。
ルジャンドル記号の性質
a
⊥
p
∧
b
⊥
p
⟹
(
a
b
p
)
=
(
a
p
)
(
b
p
)
{\displaystyle a\perp p\land b\perp p\implies ({\dfrac {ab}{p}})=({\dfrac {a}{p}})({\dfrac {b}{p}})}
平方剰余の相互法則
異なる奇素数
p
,
q
{\displaystyle p,q}
(
q
p
)
(
p
q
)
=
(
−
1
)
p
−
1
2
⋅
q
−
1
2
{\displaystyle ({\dfrac {q}{p}})({\dfrac {p}{q}})=(-1)^{{\frac {p-1}{2}}\cdot {\frac {q-1}{2}}}}
この定理から、2つの合同方程式 (合同式に関する方程式)
x
2
≡
p
(
m
o
d
q
)
{\displaystyle x^{2}\equiv p(\mathrm {mod} ~q)}
x
2
≡
q
(
m
o
d
p
)
{\displaystyle x^{2}\equiv q(\mathrm {mod} ~p)}
平方剰余の第一補充則
(
−
1
p
)
=
(
−
1
)
p
−
1
2
{\displaystyle ({\dfrac {-1}{p}})=(-1)^{\frac {p-1}{2}}}
平方剰余の第二補充則
(
2
p
)
=
(
−
1
)
p
2
−
1
8
{\displaystyle ({\dfrac {2}{p}})=(-1)^{\frac {p^{2}-1}{8}}}
1254で割って657余る平方数は存在するか。
完全剰余系の基本定理
正の合成数
n
{\displaystyle n}
a
{\displaystyle a}
n
⊥
a
{\displaystyle n\perp a}
a
,
2
a
,
3
a
,
⋯
n
a
{\displaystyle a,2a,3a,\cdots na}
n
{\displaystyle n}
n
{\displaystyle n}
i
,
j
(
1
≦
i
≦
j
≦
n
)
{\displaystyle i,j(1\leqq i\leqq j\leqq n)}
i
a
≡
j
a
{\displaystyle ia\equiv ja}
(
j
−
i
)
a
≡
0
{\displaystyle (j-i)a\equiv 0}
a
⊥
n
{\displaystyle a\perp n}
0
≦
j
−
i
≦
n
−
1
{\displaystyle 0\leqq j-i\leqq n-1}
(
j
−
i
)
a
≢
0
{\displaystyle (j-i)a\not \equiv 0}
フェルマーの小定理
p
{\displaystyle p}
a
{\displaystyle a}
a
⊥
p
{\displaystyle a\perp p}
p
{\displaystyle p}
a
p
−
1
≡
1
(
⟺
a
p
≡
a
)
{\displaystyle a^{p-1}\equiv 1(\iff a^{p}\equiv a)}
p
{\displaystyle p}
完全剰余系の基本定理より、
a
,
2
a
,
3
a
,
⋯
,
(
p
−
1
)
a
{\displaystyle a,2a,3a,\cdots ,(p-1)a}
p
{\displaystyle p}
1
,
2
,
3
,
⋯
p
−
1
{\displaystyle 1,2,3,\cdots p-1}
a
×
2
a
×
3
a
×
⋯
×
(
p
−
1
)
a
≡
1
×
2
×
3
×
⋯
×
p
−
1
⟺
a
p
−
1
(
p
−
1
)
!
≡
(
p
−
1
)
!
{\displaystyle a\times 2a\times 3a\times \cdots \times (p-1)a\equiv 1\times 2\times 3\times \cdots \times p-1\iff a^{p-1}(p-1)!\equiv (p-1)!}
ここで、
p
⊥
(
p
−
1
)
!
{\displaystyle p\perp (p-1)!}
(
p
−
1
)
!
{\displaystyle (p-1)!}
a
p
−
1
≡
1
{\displaystyle a^{p-1}\equiv 1}
オイラーの定理
m
{\displaystyle m}
m
{\displaystyle m}
φ
(
m
)
{\displaystyle \varphi (m)}
オイラーのトーシェント関数 )。
m
≧
2
{\displaystyle m\geqq 2}
a
{\displaystyle a}
m
{\displaystyle m}
a
φ
(
m
)
≡
1
(
m
o
d
m
)
{\displaystyle a^{\varphi (m)}\equiv 1(\mathrm {mod} ~m)}
1000以下の素数の個数は250以下であることを示せ。(2021年 一橋大学 問題1)
1050
=
2
1
3
1
5
2
7
1
{\displaystyle 1050=2^{1}3^{1}5^{2}7^{1}}
オイラーのトーシェント関数を用いると
φ
(
1050
)
=
1050
(
1
−
1
2
)
(
1
−
1
3
)
(
1
−
1
5
)
(
1
−
1
7
)
=
240
{\displaystyle \varphi (1050)=1050(1-{\frac {1}{2}})(1-{\frac {1}{3}})(1-{\frac {1}{5}})(1-{\frac {1}{7}})=240}
よって、1000以下の素数の個数は250以下。
方程式の数よりも変数の数の方が多く、解が無数に存在するような方程式を不定方程式 という。不定方程式の具体的な解を特殊解 、全ての解を任意の定数を用いて表したものを一般解 という。不定方程式を解く とは、整数や有理数の範囲で一般解を求めることである。
なお、連立一次方程式が無数の解を持つ条件はこちら に詳しい。
不定方程式のうち、整数係数であるものを特にディオファントス方程式 という。
x
=
a
∧
y
=
b
{\displaystyle x=a\land y=b}
{
x
=
a
y
=
b
{\displaystyle {\begin{cases}x=a\\y=b\end{cases}}}
(
x
,
y
)
=
(
a
,
b
)
{\displaystyle (x,y)=(a,b)}
(
x
y
)
=
(
a
b
)
{\displaystyle {\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}a\\b\end{pmatrix}}}
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
a
,
b
{\displaystyle a,b}
c
{\displaystyle c}
x
,
y
{\displaystyle x,y}
一次不定方程式 と呼ばれる。
整数論の基本定理
a
x
+
b
y
=
1
{\displaystyle ax+by=1}
⟺
a
⊥
b
{\displaystyle \iff a\perp b}
十分条件「
a
x
+
b
y
=
1
{\displaystyle ax+by=1}
⟹
a
⊥
b
{\displaystyle \implies a\perp b}
a
⊥
b
⟺
g
c
d
(
a
,
b
)
=
1
{\displaystyle a\perp b\iff \mathrm {gcd} (a,b)=1}
g
c
d
(
a
,
b
)
>
1
⟹
a
x
+
b
y
=
1
{\displaystyle \mathrm {gcd} (a,b)>1\implies ax+by=1}
a
{\displaystyle a}
b
{\displaystyle b}
d
{\displaystyle d}
a
x
+
b
y
{\displaystyle ax+by}
x
,
y
{\displaystyle x,y}
d
{\displaystyle d}
必要条件「
a
⊥
b
⟹
a
x
+
b
y
=
1
{\displaystyle a\perp b\implies ax+by=1}
b
≧
1
{\displaystyle b\geqq 1}
b
=
1
{\displaystyle b=1}
(
x
,
y
)
=
(
0
,
1
)
{\displaystyle (x,y)=(0,1)}
b
≧
2
{\displaystyle b\geqq 2}
a
,
2
a
,
3
a
,
⋯
b
a
{\displaystyle a,2a,3a,\cdots ba}
b
{\displaystyle b}
k
a
≡
1
(
m
o
d
b
)
{\displaystyle ka\equiv 1(\mathrm {mod} ~b)}
k
(
<
b
)
{\displaystyle k(<b)}
k
a
{\displaystyle ka}
b
{\displaystyle b}
l
{\displaystyle l}
k
a
=
b
l
+
1
{\displaystyle ka=bl+1}
k
a
−
b
l
=
1
{\displaystyle ka-bl=1}
(
k
,
−
l
)
{\displaystyle (k,-l)}
a
x
+
b
y
{\displaystyle ax+by}
べズーの補題
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
⟺
g
c
d
(
a
,
b
)
|
c
{\displaystyle \iff \mathrm {gcd} (a,b)|c}
十分条件「
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
⟹
g
c
d
(
a
,
b
)
|
c
{\displaystyle \implies \mathrm {gcd} (a,b)|c}
g
c
d
(
a
,
b
)
|
a
,
g
c
d
(
a
,
b
)
|
b
{\displaystyle \mathrm {gcd} (a,b)|a,\mathrm {gcd} (a,b)|b}
(
m
,
n
)
{\displaystyle (m,n)}
g
c
d
(
a
,
b
)
|
a
m
+
b
n
{\displaystyle \mathrm {gcd} (a,b)|am+bn}
g
c
d
(
a
,
b
)
|
c
{\displaystyle \mathrm {gcd} (a,b)|c}
必要条件「
g
c
d
(
a
,
b
)
|
c
⟹
a
x
+
b
y
=
c
{\displaystyle \mathrm {gcd} (a,b)|c\implies ax+by=c}
a
=
α
g
c
d
(
a
,
b
)
,
b
=
β
g
c
d
(
a
,
b
)
{\displaystyle a=\alpha \mathrm {gcd} (a,b),b=\beta \mathrm {gcd} (a,b)}
α
⊥
β
{\displaystyle \alpha \perp \beta }
α
m
+
β
n
=
1
{\displaystyle \alpha m+\beta n=1}
g
c
d
(
a
,
b
)
{\displaystyle \mathrm {gcd} (a,b)}
a
m
+
b
n
=
g
c
d
(
a
,
b
)
{\displaystyle am+bn=\mathrm {gcd} (a,b)}
g
c
d
(
a
,
b
)
|
c
{\displaystyle \mathrm {gcd} (a,b)|c}
c
{\displaystyle c}
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
このとき、
g
c
d
(
a
,
b
)
{\displaystyle \mathrm {gcd} (a,b)}
a
x
+
b
y
{\displaystyle ax+by}
①諳算で求める方法
例えば
7
x
+
3
y
=
1
{\displaystyle 7x+3y=1}
(
x
,
y
)
=
(
1
,
−
2
)
{\displaystyle (x,y)=(1,-2)}
67
x
+
20
y
=
3
{\displaystyle 67x+20y=3}
67
=
20
⋅
3
+
7
{\displaystyle 67=20\cdot 3+7}
20
=
7
⋅
2
+
6
{\displaystyle 20=7\cdot 2+6}
7
=
6
⋅
1
+
1
{\displaystyle 7=6\cdot 1+1}
移行するとそれぞれ以下のようになる。
7
=
67
−
20
⋅
3
{\displaystyle 7=67-20\cdot 3}
6
=
20
−
7
⋅
2
{\displaystyle 6=20-7\cdot 2}
1
=
7
−
6
⋅
1
{\displaystyle 1=7-6\cdot 1}
逆に辿って代入すると、以下のようになる。
1
=
7
−
6
⋅
1
{\displaystyle 1=7-6\cdot 1}
=
7
−
(
20
−
7
⋅
2
)
⋅
1
{\displaystyle =7-(20-7\cdot 2)\cdot 1}
=
7
⋅
3
−
20
⋅
1
{\displaystyle =7\cdot 3-20\cdot 1}
=
(
67
−
20
⋅
3
)
⋅
3
−
20
⋅
1
{\displaystyle =(67-20\cdot 3)\cdot 3-20\cdot 1}
=
67
⋅
3
+
20
⋅
(
−
10
)
{\displaystyle =67\cdot 3+20\cdot (-10)}
両辺を3倍すると、
3
=
67
⋅
9
+
20
⋅
(
−
30
)
{\displaystyle 3=67\cdot 9+20\cdot (-30)}
よって、整数解の一つは
(
x
,
y
)
=
(
9
,
−
30
)
{\displaystyle (x,y)=(9,-30)}
52
x
+
19
y
=
1
{\displaystyle 52x+19y=1}
52
=
19
⋅
2
+
14
{\displaystyle 52=19\cdot 2+14}
14
x
+
19
(
2
x
+
y
)
=
1
{\displaystyle 14x+19(2x+y)=1}
19
=
14
⋅
1
+
5
{\displaystyle 19=14\cdot 1+5}
14
(
3
x
+
y
)
+
5
(
2
x
+
y
)
=
1
{\displaystyle 14(3x+y)+5(2x+y)=1}
{
3
x
+
y
=
4
2
x
+
y
=
−
11
{\displaystyle {\begin{cases}3x+y=4\\2x+y=-11\end{cases}}}
(
x
,
y
)
=
(
15
,
−
41
)
{\displaystyle (x,y)=(15,-41)}
67
x
−
60
y
=
1
{\displaystyle 67x-60y=1}
60
=
2
2
3
1
5
1
{\displaystyle 60=2^{2}3^{1}5^{1}}
67
{\displaystyle 67}
67
x
−
60
y
≡
0
+
7
y
≡
1
{\displaystyle 67x-60y\equiv 0+7y\equiv 1}
67
⊥
10
{\displaystyle 67\perp 10}
70
x
≡
3
x
≡
10
{\displaystyle 70x\equiv 3x\equiv 10}
67
⊥
2
{\displaystyle 67\perp 2}
6
x
≡
20
{\displaystyle 6x\equiv 20}
7
y
−
6
y
≡
1
−
20
{\displaystyle 7y-6y\equiv 1-20}
y
≡
−
19
{\displaystyle y\equiv -19}
y
=
−
19
{\displaystyle y=-19}
x
=
−
17
{\displaystyle x=-17}
注意)
a
x
+
b
y
≡
c
{\displaystyle ax+by\equiv c}
まずは以下の定理を証明する。
ユークリッドの補題
a
,
b
,
k
{\displaystyle a,b,k}
a
⊥
b
∧
b
|
a
k
⟹
b
|
k
{\displaystyle a\perp b\land b|ak\implies b|k}
a
⊥
b
{\displaystyle a\perp b}
p
a
+
q
b
=
1
{\displaystyle pa+qb=1}
p
,
q
{\displaystyle p,q}
両辺に
k
{\displaystyle k}
k
p
a
+
k
q
b
=
k
{\displaystyle kpa+kqb=k}
a
k
{\displaystyle ak}
k
{\displaystyle k}
b
{\displaystyle b}
b
{\displaystyle b}
b
|
k
{\displaystyle b|k}
ユークリッドの補題を最小公倍数・最大公約数の関係を用いて証明せよ。
a
X
=
b
Y
(
a
⊥
b
)
{\displaystyle aX=bY(a\perp b)}
k
{\displaystyle k}
(
X
,
Y
)
=
(
b
k
,
a
k
)
{\displaystyle (X,Y)=(bk,ak)}
整数論の基本定理より
a
m
+
b
n
=
1
(
a
⊥
b
)
{\displaystyle am+bn=1(a\perp b)}
m
,
n
{\displaystyle m,n}
a
x
+
b
y
=
c
(
a
⊥
b
)
{\displaystyle ax+by=c(a\perp b)}
(
x
,
y
)
=
(
c
m
,
c
n
)
{\displaystyle (x,y)=(cm,cn)}
a
x
+
b
y
=
c
(
a
⊥
b
)
{\displaystyle ax+by=c(a\perp b)}
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
(
x
,
y
)
=
(
α
,
β
)
{\displaystyle (x,y)=(\alpha ,\beta )}
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
a
α
+
b
β
=
c
{\displaystyle a\alpha +b\beta =c}
a
(
x
−
α
)
=
−
b
(
y
−
β
)
{\displaystyle a(x-\alpha )=-b(y-\beta )}
ユークリッドの補題より(1)の解は整数
k
{\displaystyle k}
{
x
−
α
=
−
b
k
y
−
β
=
a
k
{\displaystyle {\begin{cases}x-\alpha =-bk\\y-\beta =ak\end{cases}}}
上の連立方程式から、一般解は
(
x
,
y
)
=
(
−
b
k
+
α
,
a
k
+
β
)
{\displaystyle (x,y)=(-bk+\alpha ,ak+\beta )}
特殊解を求める→
a
X
=
b
Y
(
a
⊥
b
)
{\displaystyle aX=bY(a\perp b)}
となる。
(
a
,
b
)
{\displaystyle (a,b)}
k
{\displaystyle k}
k
{\displaystyle k}
媒介変数 (もしくはパラメータ )といい、媒介変数を用いて変数を表すことを媒介変数表示 (もしくはパラメータ表示 )という。
媒介変数については数学Cのベクトル 、二次曲線 に詳しい。
問題
以下の一次不定方程式を解け。
17
x
+
3
y
=
9
{\displaystyle 17x+3y=9}
178
x
+
23
y
=
5
{\displaystyle 178x+23y=5}
133
x
−
30
y
=
7
{\displaystyle 133x-30y=7}
1312
−
597
y
=
11
{\displaystyle 1312-597y=11}
9で割ると7余り、11で割ると3余るような自然数のうち1000に最も近いものを求めよ。
二次式で表された不定方程式を二次不定方程式 という。
x
y
=
2
{\displaystyle xy=2}
(
x
,
y
)
=
(
1
,
2
)
,
(
−
1
,
−
2
)
,
(
2
,
1
)
,
(
−
2
,
−
1
)
{\displaystyle (x,y)=(1,2),(-1,-2),(2,1),(-2,-1)}
(
x
+
a
)
(
y
+
b
)
=
c
{\displaystyle (x+a)(y+b)=c}
(
x
+
a
,
y
+
b
)
{\displaystyle (x+a,y+b)}
c
{\displaystyle c}
方程式
x
y
+
3
x
−
5
y
+
9
=
0
{\displaystyle xy+3x-5y+9=0}
a
x
y
+
b
x
+
c
y
+
d
=
0
{\displaystyle axy+bx+cy+d=0}
(
a
x
+
p
)
(
a
y
+
q
)
=
r
{\displaystyle (ax+p)(ay+q)=r}
方程式
3
x
y
−
5
x
+
2
y
−
8
=
0
{\displaystyle 3xy-5x+2y-8=0}
a
x
2
+
b
x
y
+
c
y
2
+
d
x
+
e
y
+
f
=
0
{\displaystyle ax^{2}+bxy+cy^{2}+dx+ey+f=0}
問題
方程式
5
x
2
+
2
x
y
+
y
2
−
4
x
+
4
y
+
7
=
0
{\displaystyle 5x^{2}+2xy+y^{2}-4x+4y+7=0}
x
{\displaystyle x}
a
y
2
+
b
y
+
c
=
0
{\displaystyle ay^{2}+by+c=0}
y
{\displaystyle y}
元の方程式の整数解を求めよ。 ペル方程式
X
2
+
D
Y
2
=
n
{\displaystyle X^{2}+DY^{2}=n}
D
{\displaystyle D}
ペル方程式の性質
n
=
1
{\displaystyle n=1}
n
=
−
1
{\displaystyle n=-1}
n
=
1
{\displaystyle n=1}
x
+
D
y
{\displaystyle x+{\sqrt {D}}y}
(
x
0
,
y
0
)
{\displaystyle (x_{0},y_{0})}
k
{\displaystyle k}
(
x
0
+
D
y
0
)
k
=
p
+
D
q
{\displaystyle (x_{0}+{\sqrt {D}}y_{0})^{k}=p+{\sqrt {D}}q}
(
p
,
q
)
{\displaystyle (p,q)}
問題
方程式
x
2
+
2
x
y
−
y
2
+
3
=
0
{\displaystyle x^{2}+2xy-y^{2}+3=0}
上の方程式を平方完成せよ。
整数解を全て求めよ。
例えば、二次不定方程式
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
a
,
b
{\displaystyle a,b}
a
,
b
{\displaystyle a,b}
k
,
l
{\displaystyle k,l}
a
=
2
k
+
1
,
b
=
2
l
+
1
{\displaystyle a=2k+1,b=2l+1}
c
2
=
(
2
k
+
1
)
2
+
(
2
l
+
1
)
2
=
(
4
k
2
+
4
k
+
1
)
+
(
4
l
2
+
4
l
+
1
)
≡
2
(
m
o
d
4
)
{\displaystyle c^{2}=(2k+1)^{2}+(2l+1)^{2}=(4k^{2}+4k+1)+(4l^{2}+4l+1)\equiv 2(\mathrm {mod} ~4)}
(
2
4
)
=
−
1
{\displaystyle ({\dfrac {2}{4}})=-1}
a
,
b
{\displaystyle a,b}
二次不定方程式
a
2
+
b
2
+
3
a
b
=
c
2
{\displaystyle a^{2}+b^{2}+3ab=c^{2}}
3
|
a
{\displaystyle 3|a}
3
|
b
{\displaystyle 3|b}
数学Ⅱ の知識を多用するため理数科向けのページ で取り扱う。
数を表す方法を記数法 という。
我々が広く用いている1、2、3・・・はアラビア数字 もしくは算用数字 と呼ばれている。
エジプトでは、数は以下のような象形文字で表されていた。
エジプトの数字(ヒエログリフ)
1
10
100
1000
10000
100000
1000000
この記数法では、1つの記号が10個集まるたびに新しい記号を用いている。
を算用数字で表せ。
3412
ローマ数字
1
2
3
4
5
6
9
10
50
100
500
1000
I
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
Ⅸ
Ⅹ
L
C
D
M
5個集まると新しい記号を用いる方法と10個集まると新しい記号を用いる方法が混在しているのが、ローマ数字の特徴である。また、足し算や引き算の考え方が用いられている。
例えば、LXXはL+X+Xで70を表す。MCDXIXはM+(D-C)+X+(X-I)で1419を表す。
2つの異なるローマ数字が小→大の順に並んだ場合、それが表す数は大きい方の数から小さい方の数を引いた値になる。基本的に4、9を表したい場合のみ用いられる。
1629をローマ数字で表せ。
MDCXXIX
10進法 である。10進法で表された数を10進数 と呼ぶ。
10進数の1234は、1×10³+2×10²+3×10¹+4×10⁰という意味である。
10進法で用いられる位は左から10⁰の位、10¹の位、10²の位、10³の位、・・・であり、各位の数字は上から順に左から右へ並べる。各位の数字は0~9の整数で、整数を10で割った余りの種類と一致する。
このように、各位の数字を上から並べて数を表す方法を位取り記数法 という。
位取り記数法において、位取りの基礎となる数のことを底 という。
時を表す単位でいうと、秒・分・時間は60進法を、日は24進法を、年は365進法を、世紀は100進法を用いている。また、英語ではダースという単位で12進法を、フランス語では数字の発音に20進法を用いている。
高等学校情報 も参照。)
2進法では、位として2⁰の位、2¹の位、2²の位、2³の位・・・を用いる。各位の数字は整数を2で割った余りである0と1が用いられる。例えば、2進数の1001は10進法では1×2³+0×2²+0×2¹+1×2⁰表すので10進数の9である。
2進数を10進数と区別するため、数字の左下に(2)をつけることがある。先ほどの9の例だと
1001
(
2
)
{\displaystyle 1001_{(2)}}
例えば、常用漢字表の一番目に記載されている「亜」をUnicodeで表すと、2進数の16桁の数字0100111010011100となる。16桁だと桁数が多くて扱いづらいため、実際には16進数に直される。
16進法では10~15はアルファベットのA~Fを用いて表されることに留意すると、2進数の0100111010011100は次のように変換できる。
右から4桁づつ区切って0100 1110 1001 1100
0100
(
2
)
=
4
=
4
(
16
)
,
1110
(
2
)
=
14
=
E
16
,
1001
(
2
)
=
9
=
9
(
16
)
,
1100
=
12
=
C
(
16
)
{\displaystyle 0100_{(2)}=4=4_{(16)},1110_{(2)}=14=\mathrm {E} _{16},1001_{(2)}=9=9_{(16)},1100=12=\mathrm {C} _{(16)}}
順番に並べて4E9C よって、「亜」のUnicodeは16進数では4E9Cである。
「亜」の旧字体「亞」はUnicodeに直すと2進数の0100111010011110になるという。これを16進数で表せ。
n進法 という。
n進数を10進数に直すのは、先ほど2進数でやった計算と似たようなことを行うだけであるから容易である。
今度は、逆に、10進数をn進数に直すことを考える。
次のような手順で求めることができる。
与えられた10進数をnで割り、商と余りを求める
求めた商をnで割り、その商と余りを求める
上の手順を商が0になるまで繰り返す
出てきた余りを逆順に並べた数が求めるn進数である なぜこの手順で上手く求められるのか簡単に解説する。
上の手順では割り算の等式が複数現れる。一番上の等式に二番目の式、三番目の式・・・と順に代入すると、nの累乗数の和が現れるが、その係数は各操作で出た余りを下から順に並べたものになる。n進数はnの累乗数を降冪の順に並べた多項式の各項の係数を左側から並べたものであるから、結局は上の手順で正しく求まる。
問題
以下の数を[]内の記数法で表せ。
67[5進法]
102[2進法]
3853[9進法]
5進数で表すと4桁になるような自然数の個数を求めよ。
5進数で表された3桁の数字がある。この数字の列を9進数としてよみかえると,元の数の3倍に8を足した数になるという。この3桁の数字を5進数で答えよ。
ガウス記号は一応高校範囲に入っているが、初めて登場する単元が数Ⅰ「数と式」だったり数A「数学と人間の活動(整数の性質)」だったり数B「数列」だったり数Ⅲ「極限」だったりと、教科書や参考書によって非常にばらつきがある。Wikibooksでは、整数と関連が深いことからこの単元で扱うことにする。
x
{\displaystyle x}
[
x
]
{\displaystyle [x]}
x
{\displaystyle x}
[
]
{\displaystyle []}
ガウス記号 という。
例えば、
[
1.5
]
=
1
,
[
−
3.2
]
=
−
4
{\displaystyle [1.5]=1,[-3.2]=-4}
ガウス記号の性質
x
,
y
{\displaystyle x,y}
n
{\displaystyle n}
[
x
+
n
]
=
[
x
]
+
n
{\displaystyle [x+n]=[x]+n}
[
x
+
y
]
≧
[
x
]
+
[
y
]
{\displaystyle [x+y]\geqq [x]+[y]}
x
≧
y
⟺
[
x
]
≧
[
y
]
{\displaystyle x\geqq y\iff [x]\geqq [y]}
上の性質を証明せよ。
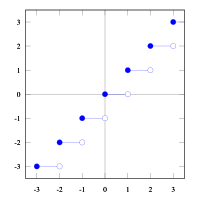
階段関数のグラフ
y
=
[
x
]
{\displaystyle y=[x]}
階段関数 という。大学では階段関数として他に天井関数や床関数が登場する。
正の実数
y
{\displaystyle y}
{
y
}
{\displaystyle \{y\}}
{
y
}
=
y
−
[
y
]
{\displaystyle \{y\}=y-[y]}
a
{\displaystyle a}
{
a
}
,
{
2
a
}
,
{
3
a
}
,
⋯
{\displaystyle \{a\},\{2a\},\{3a\},\cdots }
{
k
a
}
=
{
l
a
}
{\displaystyle \{ka\}=\{la\}}
(
k
,
l
)
{\displaystyle (k,l)}
このとき、小数部分が等しいので
k
a
−
l
a
=
N
{\displaystyle ka-la=N}
N
{\displaystyle N}
k
−
l
(
≠
0
)
{\displaystyle k-l(\neq 0)}
a
=
N
k
−
l
{\displaystyle a={\frac {N}{k-l}}}
k
−
l
{\displaystyle k-l}
a
{\displaystyle a}
{
k
a
}
=
{
l
a
}
{\displaystyle \{ka\}=\{la\}}
(
k
,
l
)
{\displaystyle (k,l)}
a
,
b
{\displaystyle a,b}
a
{\displaystyle a}
b
{\displaystyle b}
平面上に点Oをとる。Oで互いに直交する2本の数直線を引く。これらの数直線をx軸 、y軸 といい、纏めて座標軸 という。このとき、点Oを原点 という。
平面上の点Pは2つの実数の組(a, b)で表される。この組(a, b)を点Pの座標 といい、P(a, b)と書く。このとき、aをx座標 、bをy座標 という。a, bとも整数である場合は点Pを格子点 という。
このように座標の定められた平面を座標平面 という。座標平面の原点の座標はO(0, 0)である。
問題
平らな広場の地点Oを原点とし、東をx軸の正方向、北をy軸の正方向とする座標平面を考える。1mを長さ1として考えたとき、以下の問に答えよ。
地点Oから西に3m、北に7m進んだ位置の座標を答えよ。
地点Oと座標が(40, 0)である地点Aに木が植えられており、直線OAより北側の地点Pに宝物がある。地点PはOからの距離が13m、Aからの距離が37mであるという。P(x, y)とおいたとき、x,yの直を求めよ。 z軸 という。x軸とy軸が定める平面をxy平面 、y軸とz軸が定める平面をyz平面 、z軸とx軸が定める平面をzx平面 という。
空間の点Pの座標は3つの実数の組(a, b, c)で定められ、P(a, b, c)と書く。このとき、cをz座標 という。
このように座標の定められた空間を座標空間 という。座標空間の原点の座標はO(0, 0, 0)である。
問題
先ほどと同様の広場について考えたとき、地点Oから東に2m、南に1m進んで真下に5m下がった位置の座標を答えよ。
座標空間に点P(a, b, c)をとる。Pからxy平面に下ろした垂線の足をQとしたとき、線分OPの長さの2乗がa²+b²+c²であることを証明せよ。 最短曲線 )の長さを距離 という。平らな空間(ユークリッド空間 )で考える際は最短経路は必ず直線となる。後述するが、曲がった空間(非ユークリッド空間 )の上で考える際は最短経路は曲線になる。ここでは平らな空間で考える。上の問題から分かるように、ある点の原点からの距離は三平方の定理から求まる。
一般に線分を平行移動しても長さは変わらないので、2点間の距離は片方の点を原点に重ねる平行移動によって得られる。座標平面上の点
A
(
a
,
b
)
B
(
c
,
d
)
{\displaystyle A(a,b)B(c,d)}
C
(
c
−
a
,
d
−
b
)
{\displaystyle C(c-a,d-b)}
A
B
¯
{\displaystyle {\overline {AB}}}
A
B
¯
=
O
C
¯
=
(
c
−
a
)
2
+
(
d
−
b
)
2
=
(
a
−
c
)
2
+
(
b
−
d
)
2
{\displaystyle {\overline {AB}}={\overline {OC}}={\sqrt {(c-a)^{2}+(d-b)^{2}}}={\sqrt {(a-c)^{2}+(b-d)^{2}}}}
2点間の距離
座標平面上の2点
A
(
x
1
,
y
1
)
,
B
(
x
2
,
y
2
)
{\displaystyle A(x_{1},y_{1}),B(x_{2},y_{2})}
A
B
¯
=
(
x
1
−
x
2
)
2
+
(
y
1
−
y
2
)
2
{\displaystyle {\overline {AB}}={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}}
A
(
x
1
,
y
1
,
z
1
)
,
B
(
x
2
,
y
2
,
z
2
)
{\displaystyle A(x_{1},y_{1},z_{1}),B(x_{2},y_{2},z_{2})}
A
B
¯
=
(
x
1
−
x
2
)
2
+
(
y
1
−
y
2
)
2
+
(
z
1
−
z
2
)
2
{\displaystyle {\overline {AB}}={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}}}}
問題
座標空間上の2点
(
4
,
2
,
5
)
,
(
8
,
7
,
1
)
{\displaystyle (4,2,5),(8,7,1)}
一般に方程式
y
=
a
x
+
b
{\displaystyle y=ax+b}
A
x
+
B
y
+
C
=
0
{\displaystyle Ax+By+C=0}
(
p
,
q
)
{\displaystyle (p,q)}
d
=
|
A
p
+
B
q
+
C
|
A
2
+
B
2
{\displaystyle d={\frac {|Ap+Bq+C|}{\sqrt {A^{2}+B^{2}}}}}
35
x
+
21
y
=
15
{\displaystyle 35x+21y=15}
w軸 とすると、四次元空間の座標を考えることができる。原点を通り四次元の座標空間の各座標軸と直交する数直線をv軸 とすると、五次元空間の座標を考えることができる。これを続けていくと、一般のn次元まで拡張できる (我々が認識できるのは三次元までなので想像しづらいが)。大学では、nを無限大に飛ばした無限次元を考える場面も存在する。
直交座標系 という。発明した数学者の名をとってデカルト座標 という場合もある。
数学Cのベクトル 及び行列 では、2本のベクトルを基底とした斜交座標系 (ベクトル空間)を扱う。(深入りするのは大学の線形代数学 からだが。)
数学Cの二次曲線 では、原点からの距離rと座標軸の正方向からの回転角θで座標を表す極座標系 を扱う。複素数の極形式 もこの極座標系の考え方を利用したものである。
三角形の3点A, B, Cを基準として座標を考える重心座標系 というものもある。重心座標では座標の成分そのものではなく、それらの比が重要となる。重心座標を利用すると、三角形の五心 に絡む問題が解きやすくなる。
coming soon...
中学校や数学A「図形の性質」で扱ったような、図形の諸性質を用いて幾何的な問題を解く分野をユークリッド幾何学 という。数学Ⅱ「図形と方程式」や数学C「平面上の曲線」で扱うような、関数の概念を用いて幾何的な問題を解く分野を解析幾何学 という。数学C「ベクトル」「複素数平面」「数学的な表現の工夫(行列)」で扱うような、代数的な計算を用いて幾何的な問題を解く分野を代数幾何学 という。どちらも座標の考え方を用いるという点で、解析幾何学と代数幾何学は似ている。大学では、さらに非ユークリッド幾何学 と呼ばれる分野が追加される。これは、簡単に言えば曲がった空間(曲面)上の図形について考察する分野である。
ここでは、非ユークリッド幾何学の一つ、球面幾何学 の初歩的な内容として球面三角法 を扱う。
coming soon...
数学史 も参照。































































































































































































































































































![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle []}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0261e8d17bc0832139076efdad67e7c0abf21cff)
![{\displaystyle [1.5]=1,[-3.2]=-4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98396cd8326ebad5d17a4b59f77ac1e760b79a97)
![{\displaystyle [x+n]=[x]+n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b34c6a64ae8876aeec3368202c2c3a2fd66e6c6a)
![{\displaystyle [x+y]\geqq [x]+[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fe8a5b49f2b074346fcb45220754c9555e51c29)
![{\displaystyle x\geqq y\iff [x]\geqq [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41d1e6189e6d52565c3965257095def6328a916e)
![{\displaystyle y=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25a674ac2a83052f1fcdfdfe13afb0bd197e1bc3)

![{\displaystyle \{y\}=y-[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ff736b857552777947140aa3603ba06c7fb3e88)




















