本項は高等学校数学IIの式と証明・高次方程式の解説である。
三次式の展開公式より、



(参考)

 について考えよう。この式を展開するとき、
について考えよう。この式を展開するとき、 の係数は、右辺の5個の
の係数は、右辺の5個の  から
から  を3回取る組み合わせに等しいから
を3回取る組み合わせに等しいから  である。
である。
この考えを拡張して

を展開する。 の項の係数は、右辺の
の項の係数は、右辺の  個の
個の  から
から  を
を  回取る組み合わせに等しいから
回取る組み合わせに等しいから  である。
である。
よって、次の式が得られる:

最後の式は数Bの数列で学ぶ総和記号  である。知らないのなら無視しても良い。
この式を 二項定理(binomial theorem) という。また、それぞれの項にかかる係数を二項係数(binomial coefficient) と呼ぶことがある。
である。知らないのなら無視しても良い。
この式を 二項定理(binomial theorem) という。また、それぞれの項にかかる係数を二項係数(binomial coefficient) と呼ぶことがある。
(I)

(II)

(II)

をそれぞれ計算せよ。
二項定理を用いて計算すればよい。実際に計算を行なうと、
(I)

(II)

(III)

となる。
すべての自然数nに対して
(I)

(II)

(III)

が成り立つことを示せ。
二項定理

についてa,bに適当な値を代入すればよい。
(I)
a = 1,b=1を代入すると、


となり確かに与えられた関係が成立することが分かる。
(II)
a=2,b=1を代入すると、


となり確かに与えられた関係が成立することが分かる。
(III)
a=1,b=-1を代入すると、


となり確かに与えられた関係が成立することが分かる。
二項定理を拡張して  を展開することを考えよう。
を展開することを考えよう。
 の項の係数は
の項の係数は  個の
個の  から
から  個の
個の  、
、 個の
個の  、
、  個の
個の  を選ぶ組合せに等しいから
を選ぶ組合せに等しいから  である。
である。
一般には同じものを含む順列と一致する。
ここでは、整式の除法と分数式について扱う。整式の除法は、整式を整数のように扱い除法を行なう計算手法のことである。実際に整数の除法と整式の除法には深いつながりがある。整式の因数分解を考えるとそれ以上因数分解できない整式が存在する。この整式を整数でいう素因数のように扱うことで整式の素因数分解が可能になる。
上では、整式が整数に対応する性質を持つことを述べた。整数についてはたがいに素な2つの整数を取ることで有理数を定義することが出来る。整式に対しても同じ事が成立ち、そのような式を分数式と呼ぶ。
分数を用いないときには、整数の除法は商と余りを用いて定義された。この時、割られる数Bは商Dと割る数A、余りRを用いて

の性質を満たすことが知られている。整式に対しても似た性質が成立ち、割られる式B(x)が商D(x)と割る式A(x)、余りR(x)を用いて、
 と書かれるとき、B(x)が、A(x)に割られたという。この時、整数の除法の性質R<Aに対応して、R(x)の次数<A(x)の次数が成立する。具体例として、x +1を、xで割ることを考える。割る式の次数が1であることから余りの次数は0となり余りは実数である必要がある。また、商がxの関数であると
と書かれるとき、B(x)が、A(x)に割られたという。この時、整数の除法の性質R<Aに対応して、R(x)の次数<A(x)の次数が成立する。具体例として、x +1を、xで割ることを考える。割る式の次数が1であることから余りの次数は0となり余りは実数である必要がある。また、商がxの関数であると
の右辺でxについて2次の項が現われ左辺と一致しなくなる。よって商は実数である。商をa、余りをrとすると上の式は、

となるが、これはa=1,r=1で成立する。よって商1,余り1である。より高次の式に対しても同じ様に答えを定めていけばよい。例として、

のような式を考える。この場合、

で、B(x)が3次、A(x)が2次であることから、D(x)は1次であり、また、R(x)は2次より小さいことから1次以下の式になる。ここで、D(x)=ax+b,R(x)=cx+dとおくと、

が得られる。右辺を展開すると、

が得られるが、xにどんな値を入れてもこの等式が成り立たなければならないので、a = 1, b = 0, -a +c = 0, -b +d = 0が得られ、結局a=c=1, b=d=0が得られる。
この方法はどの除法に対しても用いることが出来るが、次数が高くなると計算が難しくなる。整数の場合と同様、整式の除法でも筆算を用いることが出来る。上の例を用いて結果だけを書くと、
のようになる。)右に書かれた式が割られる式であり、)左に書かれた式が割る式である。--の一番上に書かれた式は商であり、整数の割り算同様左に書かれた数から順に割っていく。ここでは次数が大きい項がより先に計算される項である。割られる式の下にある式は商の第1項を割る式にかけて得る式である。ここでは、 で、
で、 となる。ただし、整数の除法と同様、位をそろえなくてはならない。その後、割られる式から
となる。ただし、整数の除法と同様、位をそろえなくてはならない。その後、割られる式から を引き、残った式を新しい割られる式として扱う。ここでは、得た式が割る式よりも低次であることから、これで計算は終了である。
を引き、残った式を新しい割られる式として扱う。ここでは、得た式が割る式よりも低次であることから、これで計算は終了である。
 、
、 を、
を、 で割った商と余りを求めよ。
で割った商と余りを求めよ。
この計算はアニメーションを使って
詳しく表示されている。計算手法は、
整数の場合の筆算と同じような手法が使える。
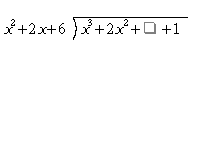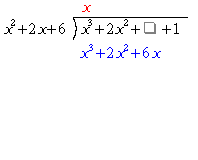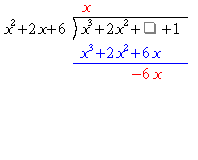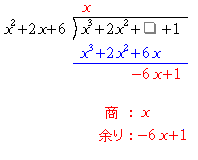 計算のアニメーション
計算のアニメーション

が得られるので、商 、余り
、余り である。
である。
2つ目の式については、

が得られる。
よって、答は
商 、余り
、余り である。
である。
ここまでで整式を整数のように扱い、整式の除法を行なう方法について述べた。ここでは、整式に対して分数式を定義する方法について述べる。分数式とは、整数に対する分数のように、除法によって生じる式である。ここで、除法を行なう式はどのようなものでも差し支えない。分数式では、分子に割られる式を書き、分母に割る式を書く。例えば、

は、分子x+1、分母 の分数式である。分数式に対しても約分や通分が存在する。約分は共通因数を持った分子分母をもつ分数式で用いられる。この時には分子分母を共通因数で割り、式を簡単にすることが出来る。通分は、分数式の加法の時によく用いられるが、分子分母に同じ整式をかけても分数式が変化しない性質を用いる。
の分数式である。分数式に対しても約分や通分が存在する。約分は共通因数を持った分子分母をもつ分数式で用いられる。この時には分子分母を共通因数で割り、式を簡単にすることが出来る。通分は、分数式の加法の時によく用いられるが、分子分母に同じ整式をかけても分数式が変化しない性質を用いる。

を簡単にせよ。また、

を計算せよ。

について分子と分母を因数分解すると、双方ともに

を因数として含んでいることが分かる。このとき、共通の因数は約分することが必要である。計算された値は、



となる。
次の問題では、

を計算する。このとき、両辺の分母をそろえる必要があるが、今回については、単純にそれぞれの分数式の分子と分母に各々の分母をかけて分母を統一すればよい。計算すると、




となる。
分数式の乗法は、分子分母を別々にかければよい。
次の計算をせよ。
(I)

(II)

(I)




(II)





分母が積の形である分数式を二つの分数式の和や差で表された式に変形する操作を部分分数分解という。
 と
と を分数式の和または差の形で表せ。
を分数式の和または差の形で表せ。

と変形できるので、

となり、約分すると

となる。
次の問題では、

と変形することによって、

となり、

と求まる。
部分分数分解の操作を逆に辿ると、分数式の通分の操作と一致する。
つまり、部分分数分解は通分の逆の操作である。
分子が定数の場合には、上と同様の方法で部分分数分解することができる。
- 問題
- 以下の分数式を部分分数分解せよ


1. 



2. 






部分分数分解は数列の和の計算、積分計算、微分を利用した不等式の証明等に役立つ、重要な変形である。
等式  は、文字
は、文字 にどのような値を代入しても成り立つ。このような等式を恒等式(こうとうしき)という。
等式
にどのような値を代入しても成り立つ。このような等式を恒等式(こうとうしき)という。
等式 は、両辺とも
は、両辺とも を代入することはできないが、その他の値であれば代入することができ、またどのような値を代入しても等式が成り立っている。これも恒等式と呼ぶ。
を代入することはできないが、その他の値であれば代入することができ、またどのような値を代入しても等式が成り立っている。これも恒等式と呼ぶ。
いっぽう、 は、x=2 または x=ー1 を代入したときだけ成り立つが、このように文字に特定の値を代入したときにだけ成り立つ式のことを方程式と呼び、恒等式とは区別する。
は、x=2 または x=ー1 を代入したときだけ成り立つが、このように文字に特定の値を代入したときにだけ成り立つ式のことを方程式と呼び、恒等式とは区別する。
等式  が
が  についての恒等式であるのはどのような場合か、考えてみよう。
ある式が「
についての恒等式であるのはどのような場合か、考えてみよう。
ある式が「  についての恒等式である」とは、この式の
についての恒等式である」とは、この式の にどのような値を代入しても、この等式は成り立つという意味である。なので、例えば
にどのような値を代入しても、この等式は成り立つという意味である。なので、例えば  に
に を代入した式
を代入した式



はすべて成り立つ必要がある。これを解くと

なので、等式  が
が  についての恒等式になるならば、
についての恒等式になるならば、 でなければならないことがわかる。
でなければならないことがわかる。
一般に、等式  が恒等式であることと、
が恒等式であることと、 が恒等式であることと同じである。
が恒等式であることと同じである。
よって
 が
が についての恒等式
についての恒等式 
 かつ
かつ  かつ
かつ 
まとめると次のようになる。
次の等式が  についての恒等式となるように、
についての恒等式となるように、 の値を求めよ。
の値を求めよ。

等式の右辺を  について整理すると
について整理すると


この等式が  についての恒等式となるのは、両辺の同じ次数の項の係数が等しいときである。よって
についての恒等式となるのは、両辺の同じ次数の項の係数が等しいときである。よって



これを解くと

- 複雑な部分分数分解(発展)
恒等式を利用することで、複雑な分数式の部分分数分解ができる。
- 問題例
- 以下の分数式を部分分数分解せよ



とおく。
分母を払って

すなわち

これが の恒等式なので、係数を比較して
の恒等式なので、係数を比較して
 かつ
かつ
すなわち

最初の等式に代入して、


次の問題は、

とおくことにより、上の問題と同様にして

と求まるので、


恒等式を利用した部分分数分解
求めたい数字を とおく。
1.
とおく。
1.  2.
2.  3.
3.  4.
4.  このようにおいた式を
このようにおいた式を の恒等式と見ることによって、
の恒等式と見ることによって、 を求められ、部分分数分解ができる。
を求められ、部分分数分解ができる。
- 2つの文字についての恒等式(発展)
a~fを定数とする。
 がx, yについての恒等式だとする。
がx, yについての恒等式だとする。
左辺をxについて整理すると、 である。
である。
これがxについての恒等式なので、 が成り立つ。
が成り立つ。
これらは更にyについての恒等式なので、以下の等式が得られる。

逆に、これが成り立てば元の式は明らかにx, yについての恒等式である
 がx,yについての恒等式となるようにa,b,c,dを定めよ。
がx,yについての恒等式となるようにa,b,c,dを定めよ。
さきほど紹介した「恒等式」という言葉を使って「証明」の意味を説明するなら、「等式を証明する」とは、その式が恒等式であることを示すことである。
一般に、等式 A=B を証明するためには、次のような手順のいずれかを実行すればよい。
- (1) Aを式変形してBを導くか、または Bを変形してAを導く。
- (2) A,Bをそれぞれ変形して、同じ式Cを導く。
- (3) A-B=0 を示す。
このとき、変形は同値変形でなければならないことに注意。
 が成り立つことを証明せよ。
が成り立つことを証明せよ。
(証明)
左辺を展開すると、
- (左辺)=

となり、これは右辺に等しい。よって、等式  は証明された。(終)
は証明された。(終)
 が成り立つことを証明せよ。
が成り立つことを証明せよ。
- (証明)
左辺を計算すると、
- (左辺) =

これは右辺に等しい。よって等式が成り立つことが証明された。(終)
次の等式が成り立つことを証明せよ。
(I)

(I)
(左辺)
(右辺)
両辺とも同じ式になるから

恒等式でないときも、与えられた条件から等式を証明することができる。
- 問題例
 のとき、
のとき、 であることを証明せよ。また、
であることを証明せよ。また、 のとき、
のとき、 を証明せよ。
を証明せよ。

より、



よって、 である。
である。
また、

より、上式の右辺をkとおくと、

なので、


よって、 である。
である。
なお、比 について
について を比の値という。また、
を比の値という。また、 を比例式という。
を比例式という。
 が成り立つとき、
が成り立つとき、 と表す。これを連比という。
と表す。これを連比という。
- 問題
 のとき、
のとき、 を満たす
を満たす を求めよ。
を求めよ。
不等式のさまざまな公式については、次の4つの式を基本的な式として導出できる場合がよくある。
高校数学では、次の4つの性質が 不等式の「基本性質」などとして紹介されている。
| 不等式の基本性質
|
- (1)
 かつ かつ  ならば ならば 
- (2)
 ならば ならば  かつ かつ 
- (3)
 かつ かつ  ならば ならば  であり、 であり、 でもある でもある
- (4)
 かつ かつ  ならば ならば  であり、 であり、 でもある でもある
|
(3)と(4)については、ひとつの性質として まとめている検定教科書もある(※ 啓林館など)。
数学IAで習った「ならば」の意味の記号  を使うと、
を使うと、
| 不等式の基本性質
|
- (1)
 かつ かつ   
- (2)
   かつ かつ 
- (3)
 かつ かつ    であり、 であり、 でもある でもある
- (4)
 かつ かつ    であり、 であり、 でもある でもある
|
とも書ける。
上述の4つの基本性質から、
- a>0, b>0 ならば a+b > 0
を証明してみよう。
(証明)
まず a>0 なので、基本性質(2)より
- a+b > b
である。
よって、
 かつ
かつ 
なので、基本性質(1)より が成り立つ。(終)
が成り立つ。(終)
同様にして、
- a<0, b<0 ならば a+b < 0
を証明できる。
- (※ 読者は自分で これを証明してみよ。検定教科書にも、この式の証明は省略されている。)
ここまでに示したことから、不等式  を証明したい場合には、
を証明したい場合には、

を証明すればよいことがわかった。こちらの方が証明しやすい場合がよくある。
不等式を証明する際に根拠とする基本的な不等式として、次の性質がある。
| 実数の2乗の性質
|
|
実数 a について、かならず

が成り立つ。
この式で等号が成り立つ場合とは、  の場合だけである。 の場合だけである。
|
この定理(「実数を2乗すると、かならずゼロ以上である」)を、基本性質(3),(4)を使って証明してみよう。
(証明)
aが正の場合と負の場合と0の場合の3通りに場合わけする。
[aが正の場合]
このとき、基本性質(3)より、

である。すなわち、

である。
[aが負の場合]
このとき、基本性質(4)より
 である。すなわち、
である。すなわち、

である。
[aがゼロの場合]
このとき、
 である。
である。
よって、すべての場合について (終)
(終)
このことと基本性質(1)(2)より、次が成り立つこともわかる。
次の不等式が成り立つことを証明せよ。

(証明)

を証明すればよい。
左辺を展開して まとめると、

となる。
上式の最後の式の項について、

だから、

である。よって

である。(終)
2つの正の数 a, b が a>b または a≧b ならば、両辺を2乗しても大小関係は同じままである。
つまり、
 ,
,  のとき、
のとき、

- これを証明するには、
 を調べればよい。
を調べればよい。

である。
a>bとする。仮定より、a,b は正の数なので、 であり、別の仮定より、 a > b なので、
であり、別の仮定より、 a > b なので、 でもある。よって、
でもある。よって、
逆に、 のとき、
のとき、 であり、
であり、 なので
なので である。よって、
である。よって、 なので、
なので、 である。
である。
よって、 である。
である。
a≧bの場合も同様に証明できる。
練習として、次の問題を問いてみよう。
- 例題
 ,
,  のとき、次の不等式を証明せよ。
のとき、次の不等式を証明せよ。

(証明)
不等式の両辺は正であるので、両辺の平方の差を考えればよい。両辺の平方の差は

である。ここで、a,b はともに正の実数なので、

であることを用いた。

であるので、

となる。よって、

である。(終)
実数 a の絶対値 |a| について、
- a ≧ 0 のとき |a|=a ,
- a<0 のとき |a|= ーa
であるから、次のことが成り立つ。
|a|≧a , |a|≧ ーa , |a|2=a2
また、2つの実数 a, b の絶対値 |ab| については、
- |ab| 2 = (ab)2 = a2 b2 = |a|2 |b|2 = (|a| |b|)2
が成り立つので、これにさらに |ab|≧0 , |a||b|≧0 を組み合わせて、
|ab| = |a| |b|
が成り立つ。
(例題)
次の不等式を証明せよ。また、等号が成り立つのは どのような場合かを 調べよ。
- |a|+|b| ≧ |a+b|
- (証明)
両辺の平方の差を考えると、
- (|a|+|b|)2 ー |a+b|2 = |a|2 + 2|a| |b| + |b|2 ー(a2 + 2ab + b2 )
- = a2 + 2|a| |b| + b2 ーa2 ー 2ab ー b2
- = 2|a| |b| ー 2ab
- = 2 ( |a| |b| ー ab )
これがもし正なら、与えられた不等式 |a|+|b| ≧ |a+b| が正しい。
ここで、 |a| |b| ≧ ab であるので、
- ( |a| |b| ー ab ) ≧ 0
である。
したがって、 |a|+|b| ≧ |a+b| である。
等号が成り立つのは |a| |b| = ab の場合、すなわち ab ≧ 0 の場合である。(証明 おわり)
三角不等式
なお
- |a|ー|b| ≦ |a+b| ≦ |a|+|b|
の関係式のことを「三角不等式」という。
2つの数 ,
, に対し、
に対し、 を相加平均(そうかへいきん)と言い、
を相加平均(そうかへいきん)と言い、 を相乗平均(そうじょうへいきん)という。
を相乗平均(そうじょうへいきん)という。
相乗平均の例と3つ以上のものの平均
平均は、3つ以上のものにも定義される。3つ以上のn個のものの相加平均は  で定義される。
で定義される。
- 平均を考える際、つい相加平均ばかりを考えがちだが、以下のような状況では相乗平均の方が適切である。
- 「ある企業では、2015年度の売上を基準にすると、2016年度では前年(2015年)の1.5倍の売上になりました。2017年度では、前年(2016年)の2倍の売上になりました。平均として、一年ごとに何倍の売り上げになっていったでしょうか? 」
- (答)
 より、約 1.73倍。
より、約 1.73倍。
- また、この応用例は、項が3つ以上の場合の相乗平均の定義の仕方も、示唆している。もし読者が指数関数を知っているなら、項が3つ(ここでは a, b, c とする)の場合の相乗平均は、
- (3つの項の相乗平均)=

- になる。
本ページでは、2個の数の平均について考察する。
相加平均と相乗平均について、次の関係式が成り立つ。
(証明)
 のとき
のとき

 であるから、
であるから、
したがって 
等号が成り立つのは、 のとき、すなわち
のとき、すなわち  のときである。(証明 おわり)
のときである。(証明 おわり)
公式の利用では、上の式  の両辺に2をかけた
の両辺に2をかけた  の形の式を使う場合もある。
の形の式を使う場合もある。
 ,
, のとき、次の不等式が成り立つことを証明せよ。
のとき、次の不等式が成り立つことを証明せよ。
(I)

(II)

(I) であるから、
であるから、
よって 
したがって

(II)

 ,
, であるから、
であるから、 ,
,
よって 
したがって

3つ以上の相乗平均と調和平均
もし読者が指数関数などを知っていれば、
n個のものの相乗平均は、
![{\displaystyle {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8f8693f03147a406583981a2c31e58260d27d1)
と書ける。
数学的な「平均」には、相加平均と相乗平均のほかにも調和平均がある。
調和平均は、電気回路の並列計算で使われる考え方である。
n個のものの調和平均は、

で定義される。
一般に数学的には、調和平均、相乗平均、相加平均のあいだに次のような大小関係
- (調和平均) ≦ (相乗平均) ≦ (相加平均)
という関係が成り立つことが証明されている。
すなわち、数式で書けば
![{\displaystyle {\frac {n}{{\dfrac {1}{a_{1}}}+{\dfrac {1}{a_{2}}}+\cdots +{\dfrac {1}{a_{n}}}}}\leqq {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}\leqq {\frac {a_{1}+a_{2}+\cdots +a_{n}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cc025ff671efd3cb148741a881d24005c56ae8a)
の関係式である。
簡潔に書くと、

となる。
一般的に使われる平均として、相加平均・相乗平均・調和平均の他に調整平均と移動平均が存在する。これらは数学B「数学と社会生活」で扱う。
2乗して負になる数、というものを考える。このような数は、中学で習った実数の中にはないことがわかる。なぜならば、正の数でも負の数でも2乗すると符号が打ち消して正の数になってしまうからである。そこで高校では、2乗して負になるという性質を持つ数の概念を新しく導入することにする。

という方程式を考える。この方程式の解は実数にはない。そこで、この方程式の解となる数を新しく作り、その単位を文字  であらわす。
であらわす。
この  のことを虚数単位(きょすうたんい)と呼ぶ。(虚数単位の記号 i 、英語のアルファベットのアイの小文字で、 imaginary unit に由来すると考えられている。)
のことを虚数単位(きょすうたんい)と呼ぶ。(虚数単位の記号 i 、英語のアルファベットのアイの小文字で、 imaginary unit に由来すると考えられている。)
 や
や  のように、虚数単位
のように、虚数単位 と実数
と実数 を用いて
を用いて

と表すことができる数を複素数(ふくそすう)という。このとき、aをこの複素数の実部(じつぶ)といい、bを虚部(きょぶ)という。
例えば、 は、いずれも複素数である。
は、いずれも複素数である。
複素数 a+bi は(ただし aとbは実数)、bが0の場合に、これを実数と見ることができる。
言い方をかえると、複素数を基準に考えると、実数とは、 a+0i のような、虚部の係数がゼロになる複素数のことであるとも言える。
4iのような、虚部が0以外で実部がゼロの複素数を純虚数(じゅんきょすう)と呼ぶ。純虚数は、2乗すると負になる数である。
実数も虚部が0の複素数と考えられる。
実数でない複素数のことを「虚数」(きょすう)という。
2つの複素数 a+bi と c+di とが等しいとは、
- a=c かつ b=d
であることである。
つまり、
- a+bi = c+di
 a=c かつ b=d
a=c かつ b=d
とくに、複素数a+bi が 0であるとは、a=0 かつ b=0 であることである。
- a+bi = 0
 a=0 かつ b=0
a=0 かつ b=0
| 複素数の相等
|
- a+bi = c+di
 a=c かつ b=d a=c かつ b=d
- a+bi = 0
 a=0 かつ b=0 a=0 かつ b=0
|
- 共役
複素数 に対して、虚部の符号を反転させた複素数
に対して、虚部の符号を反転させた複素数 のことを「共役(きょうやく)な複素数」または「複素数
のことを「共役(きょうやく)な複素数」または「複素数 の共役」のように呼び、
の共役」のように呼び、  であらわす。なお、「共役」は「共軛」の常用漢字による書き換えである。
であらわす。なお、「共役」は「共軛」の常用漢字による書き換えである。
実数aと共役な複素数は、その実数 a 自身である。
複素数 z=a+bi について


- 四則演算
複素数にも四則演算(加減乗除)が定義される。
複素数の演算では、虚数単位 を、通常の文字のように扱って計算する。一般に複素数
を、通常の文字のように扱って計算する。一般に複素数 が、
が、 で与えられるとき(ただし
で与えられるとき(ただし  は実数とする)、
は実数とする)、
- 加法

- 減法

- 乗法

- 除法
 (ただし
(ただし  とする。)
とする。)
というふうに複素数の加減乗除の計算法が定められている。
乗法の定義は、一見すると難しそうにみえるが、実数の分配法則と同様に展開していき最後に i2にマイナス1を代入していっただけである。
除法の定義は、分子と分母に、分母と共役な形の式を 掛け算 しただけである。
乗法や除法の定義式を暗記する必要は無く、計算の際には、必要に応じて分配法則や共役などの、必要な式変形を行えばいい。
例題
2つの複素数


について、 と
と  と
と  を、それぞれ計算せよ。
を、それぞれ計算せよ。
解答


である。

を、さらに簡単にできないだろうか。実は、ちょっとしたテクニックを用いればより見やすい形にできる。
分数は分母と分子に同じ数をかけてよかったので、分母と分子に分母の共役をかけてみる。すると、

が得られる。この形のほうが元の式よりもずっと見やすい形である。
このような操作を分母の実数化ということもある。数学Iで学習した展開・因数分解公式  の簡単な応用である。
の簡単な応用である。
数の範囲を複素数にまで拡張すると、負の数の平方根も考えることができる。
例として、 -5 の平方根について考えてみよう。


であるから、 -5 の平方根は  と
と  である。
である。
 とは、
とは、 のこととする。
のこととする。 とは、
とは、 のことである。
とくに
のことである。
とくに  である。
である。
さて、-5 の平方根は、方程式 の解でもある。
の解でもある。
この方程式を移項することにより、-5 の平方根は、

の解であるともいえる。
さらに因数分解をすることにより、-5 の平方根は方程式

の解でもあるともいえる。
(I)  を計算せよ。
を計算せよ。
(I)

このように、まず、マイナスの数の平方根が出てきたら、まず虚数単位 i を用いた式に書き換える。
そのあと、かけ算をしていく。
(II)  を計算せよ。
を計算せよ。
(III) 2次方程式  を解け。
を解け。
(II)

(III)



複素数の応用として、ここでは2次方程式の性質について述べる。任意の2次方程式は、解の公式によって解かれることを高等学校数学Iで述べた。しかし、解の公式に含まれる根号の中身が負の数の場合には実数解が存在しないことに注意する必要がある。2次方程式

の解の公式は、

である。
判別式 は
は

によって定義される。判別式は、解の公式の根号(ルート記号のこと)の中身に等しく、判別式の正負によって2次方程式が実数解を持つかどうかが決まる。
 が負のときにはこの2次方程式は実数の範囲には解を持たない。
が負のときにはこの2次方程式は実数の範囲には解を持たない。
判別式 が負の数であったとき、xの解は異なる2つの虚数になり、その2つの解は 共役 の関係になっている。
が負の数であったとき、xの解は異なる2つの虚数になり、その2つの解は 共役 の関係になっている。
複素数を用いて、2次方程式
(1)

(2)

(3)

を解け。
解の公式を用いて解けばよい。(1)だけを計算すると、


となる。
他も同じように扱うことが出来る。
以降の解答は、
(2)

(3)

となる。
方程式の解で、実数であるものを 実数解 という。
方程式の解で、虚数であるものを 虚数解 という。
2次方程式  の解は
の解は  である。
である。
2次方程式の解の種類は、解の公式の中の根号の中の式  の符号を見れば判別することができる。
の符号を見れば判別することができる。
この式  を、2次方程式
を、2次方程式  の判別式(はんべつしき)といい、記号
の判別式(はんべつしき)といい、記号  で表す。
で表す。
また、重解も実数解であるので、
 実数解をもつ
実数解をもつ
といえる。
次の2次方程式の解を判別せよ。
(I)

(II)

(III)

(I)

だから、異なる2つの実数解をもつ。
(II)

だから、異なる2つの虚数解をもつ。
(III)

だから、重解をもつ。
また、2次方程式  のとき、
のとき、 となるので、
2次方程式
となるので、
2次方程式  の判別式には
の判別式には

をもちいてもよい。
これを用いて、前の問題
- (III)

の解を判別しよう。
 であるから
であるから

だから、重解をもつ。
2次方程式  の2つの解を
の2つの解を  ,
, とする。 この方程式は、
とする。 この方程式は、

と変形できる。
これを展開すると、

係数を比較して、

を得る。
これを変形すれば、 となる。
となる。
2次方程式  の2つの解を
の2つの解を  ,
, とするとき、
とするとき、 の値を求めよ。
の値を求めよ。
解と係数の関係より、
 ,
,

2つの数  ,
, を解とする2次方程式は
を解とする2次方程式は

と表される。左辺を展開して整理すると次のようになる。
次の2数を解とする2次方程式を作れ。
(I)

(II)

(I)
和 
積  であるから
であるから

(II)
和 
積  であるから
であるから

2次方程式  の2つの解
の2つの解  ,
, がわかると、2次式
がわかると、2次式

を因数分解することができる。
解と係数の関係  ,
, から、
から、

2次方程式は、複素数の範囲で考えるとつねに解をもつから、複素数まで使ってよいとすると、2次式は必ず1次式の積に因数分解することができる。
複素数の範囲で考えて、次の2次式を因数分解せよ。
(I)

(II)

(I)
2次方程式  の解は
の解は

よって

(II)
2次方程式  の解は
の解は

よって

3次以上の整式による方程式を考える。
一般に方程式を  ととる。
ただし、
ととる。
ただし、 は、任意の次数の整式とする。
は、任意の次数の整式とする。
 を1次式
を1次式 で割ったときの商を
で割ったときの商を 、余りを
、余りを とすると、
とすると、

この両辺の に
に を代入すると、
を代入すると、

つまり、 を
を で割ったときの余りは
で割ったときの余りは である。
である。
整式  を次の式で割った余りを求めよ。
を次の式で割った余りを求めよ。
(I)

(II)

(III)

(I) 
(II) 
(III) 
ある実数 に対して、
に対して、

が成り立ったとする。
このとき、整式 は、
は、  を因数に持つことが分る。
このことを因数定理(いんすうていり)と呼ぶ。
を因数に持つことが分る。
このことを因数定理(いんすうていり)と呼ぶ。
整式 に対して、商
に対して、商 、割る式
、割る式 とする
整式の除法を用いる。このとき、商
とする
整式の除法を用いる。このとき、商 、
(
、
( は、
は、 よりも1だけ次数が低い整式である。)
余り
よりも1だけ次数が低い整式である。)
余り (
( は、実数。)とすると、
整式
は、実数。)とすると、
整式 は、
は、

と書ける。
ここで、  でないと、
でないと、  は満たされないが、
このとき、
は満たされないが、
このとき、 は、
は、 によって割り切れる。
よって、因数定理は成立する。
によって割り切れる。
よって、因数定理は成立する。
因数定理を用いることで、より次数の高い整式を因数分解することが
出来るようになる。例えば、3次の整式

について、 を代入すると、
を代入すると、

は0となる。よって、因数定理よりこの式は

を因数として持つ。
ここで、実際整式の除法を使って計算すると、

が得られる。
因数定理を用いて
(I)

(II)

を因数分解せよ。
(I)
因数分解の結果が(x+整数)の積の形なら、整数は6の因数でなければならない。そのため、 が候補となる。これらについては実際に代入して確かめるしかない。x=1を代入すると、
が候補となる。これらについては実際に代入して確かめるしかない。x=1を代入すると、

となるので、(x-1)が因数となる。実際に整式の除法を行なうと、商として が得られるが、これは
が得られるが、これは に因数分解できる。よって答えは、
に因数分解できる。よって答えは、

となる。
(II)
ここでも地道に24の因数を当てはめていくしかない。24の因数は数が多いのでかなりの計算が必要となる。ここでは、-2を代入すると、

となり、(x+2)が因数だとわかる。除法を行なうと、 が得られるが、(x-4)(x+3)に因数分解できる。答えは、
が得られるが、(x-4)(x+3)に因数分解できる。答えは、

となる。
因数分解や因数定理を利用して高次方程式を解いてみよう。
高次方程式
(I)

(II)

(III)

を解け。
(I)
左辺を を用いて因数分解すると
を用いて因数分解すると

したがって または
または
よって

(II)  とおくと、
とおくと、

左辺を因数分解すると

よって 
ゆえに 
したがって

(III)  とおく。
とおく。

したがって、 は
は の因数である。
の因数である。

よって 
 または
または
したがって

3次方程式  の3つの解を 、
の3つの解を 、 とすると
とすると

が成り立つ。
右辺を展開すると



よって

ゆえに

したがって、次のことが成り立つ。
しばしば虚数は「現実には存在しない数」であると言われることがあり、歴史的にも虚数を扱った数学を考えるべきではないと考えられた時代は長かった。その時代の先進的な数学者の中には、虚数を有効に活用して研究を進める一方で、成果を発表する際には虚数を表に出さずに記述する努力をすることで、無用な抵抗を受けないように工夫した者もいたと言われるほどである。
だが、よく考えてみれば、数が「現実に存在する」とはどういう意味なのだろうか。現実に鉛筆を使って紙に円を描くならば、円周の長さを「正確に円周率そのものにする」ことは不可能であるように思われるが、その割に円周率という実数は「存在する」と感じられるのはなぜだろうか。数直線が実数の「実在」を信じさせるならば、複素数は複素数平面(数学Cで習う)の上に存在するのだから、同じではないだろうか。
このように考えると、そもそも数とはすべてある意味で想像上の存在であり、それに対して「存在する」「存在しない」という問いを立てることがナンセンスであるように思われる。「存在しない」ように思われがちな虚数であるが、たとえば物理学の一分野である量子力学のシュレディンガー方程式に表れるなど、応用上のさまざまな場面においても、虚数を使って記述することが自然な対象は多いのだ。
複素数どうしについて、その大小関係は定義しない。その理由は、どのように大小関係を定義しても、便利な性質を満たすことができないからである。具体的に言えば、既に述べた実数の大小関係についての「不等式の基本性質(1)(2)(3)(4)」にあたる式を成り立たせることができないのだ。
たとえば、 であることを、
であることを、 であることとして定義してみよう。このように定義すると、たとえば1+2i<2-3iであり、また2+3i<3+4iである。ところが、(1+2i)+(2+3i)=3+5i,(2-3i)+(3+4i)=5+iであり、3+5i>5+iとなってしまう。これは基本性質(2)が成り立たないことを意味する。
であることとして定義してみよう。このように定義すると、たとえば1+2i<2-3iであり、また2+3i<3+4iである。ところが、(1+2i)+(2+3i)=3+5i,(2-3i)+(3+4i)=5+iであり、3+5i>5+iとなってしまう。これは基本性質(2)が成り立たないことを意味する。
もちろんこれは適当に考えた定義がたまたま不適切だったというだけのことだが、実は、他にどのように定義してもこのような困難からは逃れられないことが知られている。それゆえに、複素数には大小関係を定義しないのである。
今度は、複素数の平方根について考えてみよう。
正の数 を考えたとき、
を考えたとき、
 の平方根は
の平方根は
 の平方根は
の平方根は
では、
 の平方根はどのように表せるだろうか。
の平方根はどのように表せるだろうか。
虚数単位 の平方根を考えると、これはzについての方程式
の平方根を考えると、これはzについての方程式  の解 z の値であるから、これを解けばよい。どのような複素数zならこの式を満たすことができるだろうか。
の解 z の値であるから、これを解けばよい。どのような複素数zならこの式を満たすことができるだろうか。
zを複素数とすると、 (x,yは実数)と表される。
(x,yは実数)と表される。

 は実数であるから、実部と虚部が共に0にならねばならないから、
は実数であるから、実部と虚部が共に0にならねばならないから、

 のとき、
のとき、 (複号同順。x,yは共に実数であるから、条件を満たす。)
(複号同順。x,yは共に実数であるから、条件を満たす。)
 のとき、
のとき、 ここで、これを満たす実数yは存在しないから不適。
ここで、これを満たす実数yは存在しないから不適。
よって、 ■
■
 を虚数単位とするとき、次の問いに答えよ。
を虚数単位とするとき、次の問いに答えよ。
- (I)
 の平方根を求めよ。
の平方根を求めよ。
- (II) 2次方程式
 を解け。
を解け。
- (III) 3次方程式
 を解け。
を解け。
- (I)

- (II)

- (III)

- 今回挙げた問題は、全て
 (x,yは実数)と置くことで求められる。(III)は、
(x,yは実数)と置くことで求められる。(III)は、 より、
より、
実部がゼロを考慮して か
か だが、虚部もゼロなので、xの値が前者のとき
だが、虚部もゼロなので、xの値が前者のとき 、後者のとき
、後者のとき となることがすぐにわかる。
となることがすぐにわかる。
2次方程式には解の公式があり、日本の中学や高校でも習う。2次方程式の解の公式を用いれば、どんな係数の2次方程式であっても解を求められる。3次方程式と4次方程式にも、解の公式は存在し、係数がどんな係数であっても解を求められる。これらの解の公式は、代数方程式論で述べているように、係数に有限回の四則演算と根号をとる操作(代数的操作)の組み合わせで表すことができる。
5次方程式では、4次以下の方程式とは状況が異なる。一般の5次方程式の解は、2次方程式や4次方程式のように、係数に有限回の四則演算と根号をとる操作の組み合わせで表すことができないのである。ただし、「できない」ことの証明は容易ではない。このことを証明するには、ガロア理論を理解する必要がある(日本の大学の標準的なカリキュラムでは、理学部数学科の学生のみが大学3年生で学ぶのが一般的な程度の理論である)。
なお、ここで言う「表すことができない」とは一般の方程式についてのことであり、特別な5次方程式の場合は簡単に解が求められる。たとえば、 は解のひとつとして
は解のひとつとして  をもつことはすぐわかる。この方程式は他の解についても三角関数を用いて簡単に表せることを高等学校数学C/複素数平面において学ぶ。
をもつことはすぐわかる。この方程式は他の解についても三角関数を用いて簡単に表せることを高等学校数学C/複素数平面において学ぶ。
「係数に有限回の四則演算と根号をとる操作の組み合わせ」に拘らなければ、一般の5次方程式の解を求める方法も存在するが、やや高度な数学を用いる必要がある。w:五次方程式に記述があるので興味のある読者は参照するとよい。
高等学校で複素数が出てくる分野はこの分野と数学C「平面上の曲線と複素数平面」のみであり、複素数の基本計算や方程式を複素数範囲で解くこと、複素数の幾何学的意味について扱っている。しかし、大学数学においては、関数の定義域・値域を複素数範囲に広げて考える「複素関数論」というものを扱う。
実数範囲での関数はx, yともに一次元の実数軸を持つため、入力値と出力値の成すグラフを考えるには二次元の座標平面で十分であった。しかし、複素数範囲での関数はx, yともに二次元の複素数平面を持つため、入力値と出力値の成すグラフを考えるには四次元の座標空間が必要であり、三次元空間に住む我々には描画することができない。そのため、複素関数論では関数のグラフを考えることは基本的にない。(ただし、出力された複素数の絶対値を考えることによって三次元グラフに落とし込むことは可能)
では何を考えるのかというと、複素関数の微分積分である。複素関数の微分に関連して「正則関数」という用語が出てくるが、複素関数論はこの正則関数というものの性質を調べる学問だと言って良い。
複素関数論は物理学の特に波動に関する分野(音・電磁気など)において活躍している。「波動方程式」や「インピーダンス」という言葉は有名だろう。
ちなみに、複素数をさらに拡張した数として「w:四元数」というものがある。この四元数はベクトルや行列と深い関わりが存在しており、深掘ると面白いのだが、いささか冗長になるため割愛する。なお、四元数をさらに拡張した八元数や十六元数という数も研究されている。
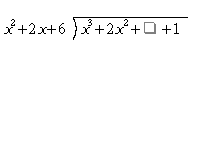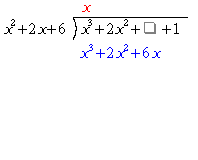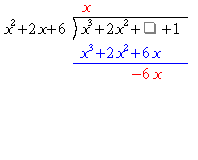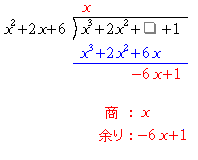
























































































































































































































































![{\displaystyle {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8f8693f03147a406583981a2c31e58260d27d1)

![{\displaystyle {\frac {n}{{\dfrac {1}{a_{1}}}+{\dfrac {1}{a_{2}}}+\cdots +{\dfrac {1}{a_{n}}}}}\leqq {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}\leqq {\frac {a_{1}+a_{2}+\cdots +a_{n}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cc025ff671efd3cb148741a881d24005c56ae8a)











































































































































































































